如图,把长方形纸片ABCD纸沿对角线折叠,设重叠部分为△EBD,那么,有下列说法:
①△EBD是等腰三角形,EB="ED" ;
②折叠后∠ABE和∠CBD一定相等;
③折叠后得到的图形是轴对称图形;
④△EBA和△EDC一定是全等三角形.
其中正确的有( )

| A.1个 | B.2个 | C.3个 | D.4个 |
如图,在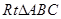 中,
中,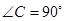 ,
,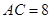 ,
,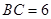 ,点
,点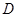 是
是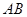 上的一个动点(不与
上的一个动点(不与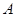 、
、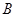 两点重合),
两点重合),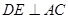 于点
于点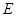 ,
,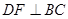 于点
于点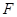 ,点
,点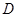 从靠近点
从靠近点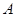 的某一点向点
的某一点向点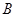 移动,矩形
移动,矩形 的周长变化情况是( )
的周长变化情况是( )
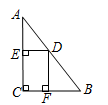
| A.逐渐减小 | B.逐渐增大 | C.先增大后减小 | D.先减小后增大 |
下列命题中,不正确的是( ).
| A.一个四边形如果既是矩形又是菱形,那么它一定是正方形 |
| B.有一个角是直角,且有一组邻边相等的平行四边形是正方形 |
| C.有一组邻边相等的矩形是正方形 |
| D.两条对角线垂直且相等的四边形是正方形 |
△ABC中,D、E、F分别是BC、CA、AB边的中点,那么四边形AFDE的周长等于( ).

(A)AB+AC (B)AD+BC (C) (D)BC+AC
(D)BC+AC
若一个正多边形的一个内角等于135°,则该多边形是正 边形,对角线有 条。 ( )
| A.8,20 | B.8,5 | C.10,20 | D.11,8 |
如图,在菱形ABCD中,AB=2,∠BAD=60°,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值为( )

| A.1 | B. |
C.2 | D. |
下列命题正确的是( )
| A.一组对边相等,另一组对边平行的四边形一定是平行四边形 |
| B.对角线相等的四边形一定是矩形 |
| C.两条对角线互相垂直的四边形一定是菱形 |
| D.两条对角线相等且互相垂直平分的四边形一定是正方形 |
如图,矩形的两条对角线的一个交角为60°,两条对角线的长度的和为20cm,则这个矩形的一条较短边的长度为( )
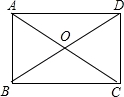
| A.10cm | B.8cm | C.6cm | D.5cm |
如图,四边形ABCD是正方形,△ADE绕着点A旋转90°后到达△ABF的位置,连接EF,则△AEF的形状是( )

| A.等腰三角形 | B.锐角三角形 | C.等腰直角三角形 | D.等边三角形 |
如图,在等腰梯形ABCD中,AB∥CD,AD=BC=acm,∠A=60°,BD平分∠ABC,则这个梯形的周长是( )

| A.4acm | B.5acm | C.6acm | D.7acm |
如图,在正方形ABCD中,E为DC边上的点,连接BE,将ΔBCE绕点C顺时针方向旋转90°得到ΔDCF,连接EF,若∠BEC=60°,则∠EFD的度数为( )

| A.10° | B.15° | C.20° | D.25° |