如图,四边形ABCD中,∠BAD=∠ACB=90°,AB=AD,AC=4BC,
设CD的长为x,四边形ABCD的面积为y,则y与x之间的函数关系式是( )
A. |
B. |
C. |
D. |
类比等腰三角形的定义,我们定义:有一组邻边相等的凸四边形叫做“等邻边四边形”.
(1)概念理解
如图1,在四边形ABCD中,添加一个条件使得四边形ABCD是“等邻边四边形”.请写出你添加的一个条件.
(2)问题探究
①小红猜想:对角线互相平分的“等邻边四边形”是菱形.她的猜想正确吗?请说明理由。
②如图2,小红画了一个Rt△ABC,其中∠ABC=90°,AB=2,BC=1,并将Rt△ABC沿∠ABC的平分线BB'方向平移得到△A'B'C',连结AA',BC'.小红要是平移后的四边形ABC'A'是“等邻边四边形”,应平移多少距离(即线段BB'的长)?
(3)应用拓展
如图3,“等邻边四边形”ABCD中,AB=AD,∠BAD+∠BCD==90°,AC,BD为对角线,AC= AB.试探究BC,CD,BD的数量关系.
AB.试探究BC,CD,BD的数量关系.
如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF、FD.
(1)求证:四边形AFDC是平行四边形;
(2)当△ABC满足什么条件时,四边形AFBD是矩形?并说明理由.
如图, 中,点 为弦 中点,连接 , , ,点 是 上任意一点,则 度数为
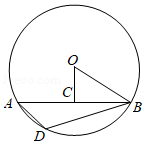
| A. |
|
B. |
|
C. |
|
D. |
|
如图,已知 为四边形 的外接圆, 为圆心,若 , ,则 的半径长为

A. B. C. D.
如图,四边形 内接于 , ,点 在 的延长线上,且 .
(1)求证: 是 的切线;
(2)若 ,当 , 时,求 的长.

如图,等腰梯形ABCD的对角线长为13,点E、F、G、H分别是边AB、BC、CD、DA的中点,则四边形EFGH的周长是( )

A.13 B.26 C.36 D.39
下列说法中,正确的是( )
| A.同位角相等 |
| B.对角线相等的四边形是平行四边形 |
| C.四条边相等的四边形是菱形 |
| D.矩形的对角线一定互相垂直 |
如图,线段AB=10,点P是AB的动点,分别以AP、BP为边在线段AB的同侧作正方形APMN、PBEF,连结ME,则ME的最小值是 .

菱形ABCD的一条对角线长为6,边AB的长为方程 ﹣7y+10=0的一个根,则菱形ABCD的周长为( )
﹣7y+10=0的一个根,则菱形ABCD的周长为( )
| A.8 | B.20 | C.8或20 | D.10 |
如图,在△ABC中,点D、E、F分别在BC、AB、CA上,且DE∥CA,DF∥BA,则下列三种说法:
(1)如果∠BAC=90°,那么四边形AEDF是矩形
(2)如果AD平分∠BAC,那么四边形AEDF是菱形
(3)如果AD⊥BC且AB=AC,那么四边形AEDF是正方形 .其中正确的有 ( )
A.3个 B.2个 C.1个 D.0个