如图,△ABC是等腰三角形,AB=BC,点D为BC的中点.
(1)用圆规和没有刻度的直尺作图,并保留作图痕迹:
①过点B作AC的平行线BP;
②过点D作BP的垂线,分别交AC,BP,BQ于点E,F,G.
(2)在(1)所作的图中,连接BE,CF.求证:四边形BFCE是平行四边形.
“赵爽弦图”是由四个全等的直角三角形与一个小正方形拼成的一个大正方形。如果小正方形的面积为4,大正方形的面积为100,直角三角形中较大的锐角为 ,则
,则 的值等于( )
的值等于( )
A. |
B. |
C. |
D. |
直角三角形的两直角边长分别是3cm和4cm,则连接两直角边的中点的线段长是 .
如图,在□ABCD中,DE平分∠ADC,AD=6,BE=2,则□ABCD的周长是( )
| A.16 | B.14 | C.20 | D.24 |
四边形ABCD的对角线AC、BD相较于点O,有下列条件①AB=AD;② ;③AO="CO" BO=DO;④矩形ABCD;⑤菱形ABCD;⑥正方形ABCD,则下列推理中,不成立的是( )
;③AO="CO" BO=DO;④矩形ABCD;⑤菱形ABCD;⑥正方形ABCD,则下列推理中,不成立的是( )
A.①④ ⑥ B.①③
⑥ B.①③ ⑤ C.①②
⑤ C.①② ⑥ D.②③
⑥ D.②③ ④
④
如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC且DE=OC, 连接 CE、OE,连接AE交OD于点F.
(1)求证:OE=CD
(2)若菱形ABCD的边长为4, ∠ABC=60°,求AE的长.
(10分)如图,四边形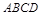 中,
中,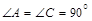 ,
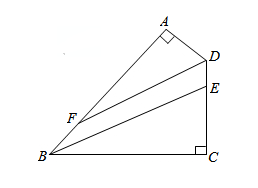
,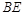 平分
平分 交
交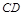 于
于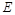 ,
,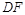 平分
平分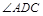 交
交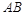 于
于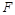 .
.
(1)若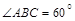 ,则
,则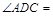 °,
°,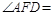 °;
°;
(2)求证:BE∥DF
利用两块长方体木块测量一张桌子的高度.首先按图①方式放置,再交换两木块的位置,按图②方式放置.测量的数据如图,则桌子的高度是 ( ) 
| A.73cm | B.74cm | C.75cm | D.76cm |
如图,在△ABC中,AB=BC,AB=12 cm,F是AB边上一点,过点F作FE∥BC交AC于点E,过点E作ED∥AB交BC于点D,则四边形BDEF的周长是 .
菱形的周长是16㎝,菱形的高是2㎝,则菱形其中一个内角的角度是( ).
| A.30° | B.45° | C.60° | D.75° |
如图3,在平面直角坐标系中,第一象限内长方形ABCD,AD∥x轴,点E在x轴上,EC交AD于G, BF平分∠CBE交OC于F,若∠CGD=2∠OCE,则下列结论正确的是( ).
| A.∠BEC=∠BFO |
| B.∠BEC+∠BFO=1350 |
C. ∠BEC+∠BFO= 900 ∠BEC+∠BFO= 900 |
D.∠BEC+ ∠BFO= 900 ∠BFO= 900 |