初中数学圆内接四边形的性质试题

如下图，□ABCD的对角线BD＝4cm，将□ABCD绕其对称中心O旋转180°，则点D所转过的路径长为  ▲  cm．

已知任意直线l把□ABCD分成两部分，要使这两部分的面积相等，直线l所在位置需满足的条件是                    ．(只需填上一个你认为合适的条件)．

在□ABCD中, ∠B—∠A＝30°，则∠A、∠B、∠C、∠D的度数分别是 (      )

A．95°、85°、95°、85°	B．85°、95°、8 5°、95°
C．105°、75°、105°、75°	D．75°、105°、75°、105°

顺次连结四边形四边中点所得的四边形一定是（   ）

A．平行四边形	B．矩形
C．菱形	D．正方形

如图1，在□ABCD中，BD＝4，将□ABCD绕其对称中心O旋转90°，则点D经过的路径长为(      )

A．4π

B．3π

C．2π

D．π

如图，小聪在作线段AB的垂直平分线时，他是这样操作的：分别以A和B为圆心，大于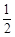AB的长为半径画弧，两弧相交于C、D，则直线CD即为所求．根据他的作图方法可知四边形ADBC一定是

A．矩形           B．菱形           C．正方形         D．等腰梯形

如图，已知E、F是□ABCD对角线AC上的两点，且BE⊥AC，DF⊥AC.
求证： BE=DF；                           

已知梯形的上底长为3cm，中位线长为6cm，则下底长为          cm。

矩形具有而菱形不一定具有的性质是               (     )

A．对角线互相垂直

B．对角线相等

C．对角线互相平分

D．对角互补

若一个正多边形的一个内角是120°，则这个正多边形的边数是（  ）

A．9

B．8

C．6

D．4

如图，E、F是□ABCD的对角线AC上的两点，且AF＝CE．请你猜想线段BE与DF之间的关系，并加以证明．                           

在四边形ABCD中,∠D=80º,∠A,∠B,∠C的度数之比为3：5：6，则最大的内角是_______度.

已知：如图，□ABCD中，BD是对角线，AE⊥BD于E，CF⊥BD于F. 求证：BE=DF.

如图，已知平行四边形ABCD中，点为边的中点，   延长相交于点．求证：

已知四边形ABCD是平行四边形，下列结论中不正确的是            （    ）

A．当AB=BC时，它是菱形	B．当AC⊥BD时，它是菱形
C．当∠ABC=90°时，它是矩形	D．当AC=BD时，它是正方形