初中数学垂径定理的应用试题

如图，是的弦，半径于点，若的半径为5，，则的长是　　

A．2B．3C．4D．5

我国古代数学经典著作《九章算术》中记载了一个“圆材埋壁”的问题：“今有圆材埋在壁中，不知大小．以锯锯之，深一寸，锯道长一尺．问径几何？”意思是：今有一圆柱形木材，埋在墙壁中，不知其大小．用锯去锯这木材，锯口深 $\mathit{ED}=1$寸，锯道长 $\mathit{AB}=1$尺 $(1$尺 $=10$寸）．问这根圆形木材的直径是　　寸．

如图，在平面直角坐标系中，⊙P与x轴相切，与y轴相交于A（0，2），B（0，8），则圆心P的坐标是（　　）

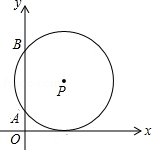
A．（5，3）B．（5，4）C．（3，5）D．（4，5）

如图将半径为 $2\mathit{cm}$的圆形纸片折叠后，圆弧恰好经过圆心 $O$，则折痕 $\mathit{AB}$的长为 $($　　 $)$

A． $2\mathit{cm}$B． $\sqrt{3}\mathit{cm}$C． $2\sqrt{5}\mathit{cm}$D． $2\sqrt{3}\mathit{cm}$

是的弦，，垂足为，连接．若中有一个角是，，则弦的长为　　．

已知 $\mathit{AB}$， $\mathit{CD}$是 $\odot O$的两条平行弦， $\mathit{AB}=8$， $\mathit{CD}=6$， $\odot O$的半径为5，则弦 $\mathit{AB}$与 $\mathit{CD}$的距离为 $($　　 $)$

A．1B．7C．4或3D．7或1

如图，一条公路的转弯处是一段圆弧 $\left(\stackrel{̂}{\mathit{AB}}\right)$ ，点 $O$ 是这段弧所在圆的圆心， $\mathit{AB}=40m$ ，点 $C$ 是 $\stackrel{̂}{\mathit{AB}}$ 的中点，点 $D$ 是 $\mathit{AB}$ 的中点，且 $\mathit{CD}=10m$ ，则这段弯路所在圆的半径为 $($ 　　 $)$

A．

$25m$

B．

$24m$

C．

$30m$

D．

$60m$

（1）如图1，有一个残缺圆，请作出残缺圆的圆心（保留作图痕迹，不写作法）．

（2）如图2，设是该残缺圆的直径，是圆上一点，的角平分线交于点，过作的切线交的延长线于点．

①求证：；

②若，，求残缺圆的半圆面积．

一块圆形宣传标志牌如图所示，点 $A$ ， $B$ ， $C$ 在 $\odot O$ 上， $\mathit{CD}$ 垂直平分 $\mathit{AB}$ 于点 $D$ ．现测得 $\mathit{AB}=8\mathit{dm}$ ， $\mathit{DC}=2\mathit{dm}$ ，则圆形标志牌的半径为 $($ 　　 $)$

A．

$6\mathit{dm}$

B．

$5\mathit{dm}$

C．

$4\mathit{dm}$

D．

$3\mathit{dm}$

如图， $\odot O$的半径 $\mathit{OA}=6$，以 $A$为圆心， $\mathit{OA}$为半径的弧交 $\odot O$于 $B$、 $C$点，则 $\mathit{BC}=($　　 $)$

A． $6\sqrt{3}$B． $6\sqrt{2}$C． $3\sqrt{3}$D． $3\sqrt{2}$

如图，在正方形纸片 $\mathit{ABCD}$中， $\mathit{EF}//\mathit{AD}$， $M$， $N$是线段 $\mathit{EF}$的六等分点，若把该正方形纸片卷成一个圆柱，使点 $A$与点 $D$重合，此时，底面圆的直径为 $10\mathit{cm}$，则圆柱上 $M$， $N$两点间的距离是　     　 $\mathit{cm}$．

已知圆的半径是10，一条弦长为16，则圆心到这条弦的距离是　　．

点 $P$ 是 $\odot O$ 内一点，过点 $P$ 的最长弦的长为 $10\mathit{cm}$ ，最短弦的长为 $6\mathit{cm}$ ，则 $\mathit{OP}$ 的长为 $($ 　　 $)$

A．

$3\mathit{cm}$

B．

$4\mathit{cm}$

C．

$5\mathit{cm}$

D．

$6\mathit{cm}$

如图是一位同学从照片上剪切下来的海上日出时的画面，"图上"太阳与海平线交于 $A$ ， $B$ 两点，他测得"图上"圆的半径为10厘米， $\mathit{AB}=16$ 厘米．若从目前太阳所处位置到太阳完全跳出海平面的时间为16分钟，则"图上"太阳升起的速度为 $($ 　　 $)$

A．

1.0厘米 $/$ 分

B．

0.8厘米 $/$ 分

C．

1.2厘米 $/$ 分

D．

1.4厘米 $/$ 分

如图， $\mathit{AB}$ 是 $\odot O$ 的弦， $\mathit{OC}\perp \mathit{AB}$ ，垂足为点 $C$ ，将劣弧 $\stackrel{̂}{\mathit{AB}}$ 沿弦 $\mathit{AB}$ 折叠交于 $\mathit{OC}$ 的中点 $D$ ，若 $\mathit{AB}=2\sqrt{10}$ ，则 $\odot O$ 的半径为 　                　．