如图,在正方形纸片 中, , , 是线段 的六等分点,若把该正方形纸片卷成一个圆柱,使点 与点 重合,此时,底面圆的直径为 ,则圆柱上 , 两点间的距离是 .

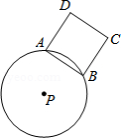
如图, 的半径为5, 、 是圆上任意两点,且 ,以 为边作正方形 (点 、 在直线 两侧).若 边绕点 旋转一周,则 边扫过的面积为 .
小华为了求出一个圆盘的半径,他用所学的知识,将一宽度为 的刻度尺的一边与圆盘相切,另一边与圆盘边缘两个交点处的读数分别是“4”和“16”(单位: ,请你帮小华算出圆盘的半径是 .

《九章算术》作为古代中国乃至东方的第一部自成体系的数学专著,与古希腊的《几何原本》并称现代数学的两大源泉.在《九章算术》中记载有一问题“今有圆材埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺,问径几何?”小辉同学根据原文题意,画出圆材截面图如图所示,已知:锯口深为1寸,锯道 尺 尺 寸),则该圆材的直径为 寸.

在周长为26π的⊙ O中, CD是⊙ O的一条弦, AB是⊙ O的切线,且 AB∥ CD,若 AB和 CD之间的距离为18,则弦 CD的长为 .
如图,两同心圆的大圆半径长为5 cm,小圆半径长为3 cm,大圆的弦 AB与小圆相切,切点为 C,则弦 AB的长是 .
