初中数学圆试题

如图，正方形的边长为，分别交于点，在上任取两点，那么图中阴影部分的面积是         ．

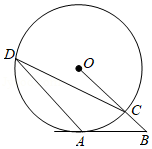
如图，已知⊙O是△ABD的外接圆，AB是⊙O的直径，CD是⊙O的弦，∠ABD=58°，则∠BCD等于（ ）

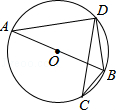
A．116°

B．32°

C．58°

D．64°

矩形具有而菱形不具有的性质是（     ）

A．对角线互相平分	B．对角线互相垂直
C．对角线相等	D．是中心对称图形

如图， $\mathit{PA}$ ， $\mathit{PB}$ 是 $\odot O$ 的切线， $A$ ， $B$ 是切点，若 $\angle P=70°$ ，则 $\angle \mathit{ABO}=($ 　　 $)$

A．

$30°$

B．

$35°$

C．

$45°$

D．

$55°$

一个多边形的内角和比它的外角和的3倍少180°，这个多边形的边数是多少？

如图，在△ABC中，∠ABC＝90°，D是边AC上的一点，连接BD，使∠A＝2∠1，E是BC上的一点，以BE为直径的圆O经过点D

（1）求证：AC是⊙O的切线；
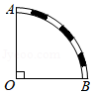
（2）若∠A＝60°，⊙O的半径为2，求阴影部分的面积（结果保留根号和π）．

如图，在正方形ABCD中，动点E，F分别从D，C两点同时出发，以相同的速度在边DC，CB上移动，连接AE和DF交于点P，由于点E，F的移动，使得点P也随之运动，若AD=2，线段CP的最小值是           ．

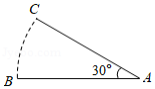
如图是圆弧形状的铁轨示意图，半径 $\mathit{OA}$ 的长度为200米，圆心角 $\angle \mathit{AOB}=90°$ ，则这段铁轨的长度为 　　米．（铁轨的宽度忽略不计，结果保留 $\pi )$

如图，线段AB是⊙O的直径，弦CD丄AB，∠CAB=20°，则∠AOD等于（  ）

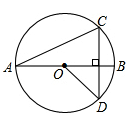
A．120°

B．140°

C．150°

D．160°

如图， $\mathit{AB}$ 是 $\odot O$ 的直径， $\mathit{AC}$ ， $\mathit{BC}$ 是 $\odot O$ 的弦，若 $\angle A=20°$ ，则 $\angle B$ 的度数为 $($ 　　 $)$

A．

$70°$

B．

$90°$

C．

$40°$

D．

$60°$

如图，将线段 $\mathit{AB}$ 绕点 $A$ 顺时针旋转 $30°$ ，得到线段 $\mathit{AC}$ ．若 $\mathit{AB}=12$ ，则点 $B$ 经过的路径 $\widehat{\mathit{BC}}$ 长度为 　　．（结果保留 $\pi )$

如图，在 $\odot O$ 中， $\mathit{AB}$ 切 $\odot O$ 于点 $A$ ，连接 $\mathit{OB}$ 交 $\odot O$ 于点 $C$ ，过点 $A$ 作 $\mathit{AD}//\mathit{OB}$ 交 $\odot O$ 于点 $D$ ，连接 $\mathit{CD}$ ．若 $\angle B=50°$ ，则 $\angle \mathit{OCD}$ 为 $($ 　　 $)$

A．

$15°$

B．

$20°$

C．

$25°$

D．

$30°$

如图， $\mathit{AB}$ 是 $\odot O$ 的直径， $\mathit{BC}$ 是 $\odot O$ 的切线，若 $\angle \mathit{BAC}=35°$ ，则 $\angle \mathit{ACB}$ 的大小为 $($ 　　 $)$

A．

$35°$

B．

$45°$

C．

$55°$

D．

$65°$

《九章算术》被尊为古代数学“群经之首”，其卷九勾股篇记载：今有圆材埋于壁中，不知大小．以锯锯之，深一寸，锯道长一尺．问径几何？如图，大意是，今有一圆柱形木材，埋在墙壁中，不知其大小，用锯去锯这木材，锯口深 $\mathit{CD}$等于1寸，锯道 $\mathit{AB}$长1尺，问圆形木材的直径是多少？ $(1$尺 $=10$寸）

答：圆材直径 　　寸．

如图，⊙O的弦AB=8，M是AB的中点，且OM=3，则⊙O的直径等于（  ）

A．5

B．8

C．10

D．12