初中数学圆试题

如图，在4×4的正方形网格中，每个小正方形的边长为1，若将△AOC绕点O顺时针旋转90°得到△BOD，则的长为（  ）

A．π

B．6π

C．3π

D．1.5π

如图，下面4个正方形的边长都相等，其中阴影部分的面积相等的图形有_________（填序号）
 

如图，⊙O的弦AB=8，M是AB的中点，且OM=3，则⊙O的直径等于（  ）

A．5

B．8

C．10

D．12

如图，在⊙O中，弧AB=60°，AB=6，

（1）求圆的半径；   
（2）求弧AB的长；
（3）求阴影部分的面积．

如图，线段AB是⊙O的直径，弦CD丄AB，∠CAB=20°，则∠AOD等于（  ）

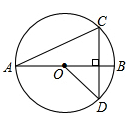
A．120°

B．140°

C．150°

D．160°

为了加快灾后重建的步伐，我市某镇要在三条公路围成的一块平地上修建一个砂石场，如图，要使这个砂石场到三条公路的距离相等，则可供选择的地址（  ）

A．仅有一处

B．有四处

C．有七处

D．有无数处

如图，沿AE折叠矩形纸片ABCD，使点D落在BC边的点F处．已知AB=8，BC=10，则tan∠EFC的值为 （   ）

A．

B．

C．

D．

五边形的内角和为________度，十二边形的外角和为_________度．

如图，四边形ABCD、DEFG都是正方形，连接AE、CG、AE与CG相交于点M，CG与AD相交于点N．

求证：（1）；
（2）

我们把两条中线互相垂直的三角形称为“中垂三角形”．例如图1，图2，图3中，AF，BE是△ABC的中线， AF⊥BE ， 垂足为P．像△ABC这样的三角形均为“中垂三角形”．设，，．
特例探索
（1）如图1，当∠=45°，时，=             ，              ；
如图2，当∠=30°，时，  =             ，              ；

归纳证明
（2）请你观察（1）中的计算结果，猜想三者之间的关系，用等式表示出来，并利用图3证明你发现的关系式；
拓展应用
（3）如图4，在□ABCD中，点E，F，G分别是AD，BC，CD的中点，BE⊥EG， AD= ，AB=3．求AF的长．

如图，在矩形ABCD中，对角线与相交于点O，且AB=OA=2cm ，则BD的长为________cm，BC的长为_______cm．

顺次连结对角线相等的四边形各边中点所得到的四边形一定是（    ）

A．平行四边形

B．矩形

C．菱形

D．正方形

如图，正方形ABCB₁中，AB=1．AB与直线l的夹角为30°，延长CB₁交直线l于点A₁，作正方形A₁B₁C₁B₂，延长C₁B₂交直线l于点A₂，作正方形A₂B₂C₂B₃，延长C₂B₃交直线l于点A₃，作正方形A₃B₃C₃B₄，…，依此规律，则A₂₀₁₄A₂₀₁₅=            ．

如果一个正多边形的中心角为45°，那么这个正多边形的边数是           ．

用形状、大小完全相等的下列图形不能进行密铺的是（ ）

A．等腰三角形	B．平行四边形
C．正五边形	D．正六边形