初中数学圆试题

已知等腰三角形的腰长为5，一腰上的高为4，则以底边为边长的正方形的面积为          ．

如图，菱形ABCD，对角线AC、BD交于点O，DE//AC，CE//BD，求证：OE=BC．

如图，正方形ABCD绕点B逆时针旋转30°后得到正方形BEFG，EF与AD相交于点H，延长DA交GF于点K．若正方形ABCD边长为，则AK=           ．

已知正方形ABCD，以CD为边作等边三角形△CDE，则∠AED的度数是            ．

如图所示，菱形ABCD中，对角线相AC、BD交于点O，H为边AD的中点，菱形ABCD的周长为36，则OH的长等于（ ）

A．4．5    B．5    C．6    D．9

意大利著名数学家斐波那契在研究兔子繁殖问题时，发现有这样一组数：1，1，2，3，5，8，13，…，其中从第三个数起，每一个数都等于它前面两个数的和．现以这组数中的各个数作为正方形的边长值构造正方形，再分别依次从左到右取2个、3个、4个、5个…正方形拼成如上长方形，若按此规律继续作长方形，则序号为⑦的长方形周长是           ．

在如图所示的3×3的方格中，画出4个面积小于9的不同的正方形，而且所画正方形的顶点都在方格的顶点上（请标上顶点的四个字母）．

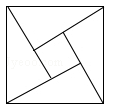
如图是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形，如果大正方形的面积是13，小正方形的面积是1，那么每个直角三角形的周长为          ．

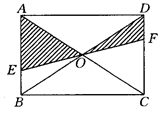
如图所示，EF过矩形ABCD对角线的交点O，且分别交AB，CD于点E，F，若AB=3，BC=4，那么阴影部分的面积为（   ）

A．4

B．12

C．6

D．3

有一根长60cm的铁丝，用它围成一个矩形，写出矩形面积S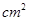（）与它的一边长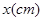之间的函数关系式为（   ）

A．

B．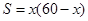

C．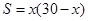

D．

如图，在3×3的正方形网格中标出了∠1和∠2．则∠1+∠2=      ．

如图，正方形ABCD的面积为16，点F在AD上，点E在AB的延长线上，FC⊥CE，△CEF的面积为12.5，则BE的值为      ．

设边长为2a的正方形的中心A在直线l上，它的一组对边垂直于直线l，半径为r的圆的圆心O在直线l上运动，A、O两点之间的距离为d．
（1）如图①，当r＜a时，填表：

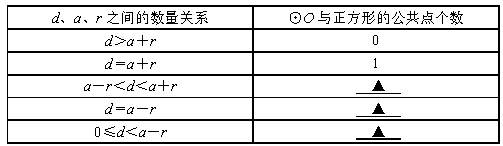
（2）如图②，⊙O与正方形有5个公共点B、C、D、E、F，求此时r与a之间的数量关系；

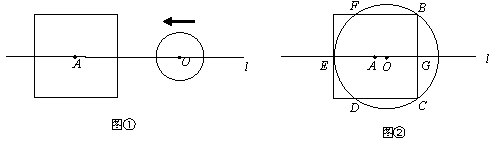
（3）由（1）可知，d、a、r之间的数量关系和⊙O与正方形的公共点个数密切相关．当r=a时，请根据d、a、r之间的数量关系，判断⊙O与正方形的公共点个数；
（4）当r与a之间满足（2）中的数量关系时，⊙O与正方形的公共点个数为    ．

正方形ABCD内一点P，BP=2，把△ABP绕点B顺时针旋转90°得到△CBP′，则PP′的长为（ ）

A．2

B．2

C．3

D．3

如图，在直角梯形ABCD中，AD∥BC，∠B=90°，且AD=12cm，AB=8cm，DC=10cm，若动点P从A点出发，以每秒2cm的速度沿线段AD向点D运动；动点Q从C点出发以每秒3cm的速度沿CB向B点运动，当P点到达D点时，动点P、Q同时停止运动，设点P、Q同时出发，并运动了t秒，回答下列问题：

（1）BC=          cm；
（2）当t为多少时，四边形PQCD成为平行四边形？
（3）当t为多少时，四边形PQCD为等腰梯形？
（4）是否存在t，使得△DQC是等腰三角形？若存在，请求出t的值；若不存在，说明理由．