如图,在矩形 中,点 , 分别在 , 上, .只需添加一个条件即可证明四边形 是菱形,这个条件可以是 (写出一个即可).

设 , , , 是反比例函数 图象上的任意四点,现有以下结论:
①四边形 可以是平行四边形;
②四边形 可以是菱形;
③四边形 不可能是矩形;
④四边形 不可能是正方形.
其中正确的是 .(写出所有正确结论的序号)
如图,在 中, , 分别平分 和 , , .若从三个条件:① ;② ;③ 中,选择一个作为已知条件,则能使四边形 为菱形的是 (填序号).

如图,在 中, , ,将它沿 翻折得到 ,则四边形 的形状是 形,点 、 、 分别为线段 、 、 的任意点,则 的最小值是 .

如图, 是 的对角线,按以下步骤作图:①分别以点 和点 为圆心,
大于 的长为半径作弧,两弧相交于 , 两点;②作直线 ,分别交 , 于点 , ,连接 , .若 , ,则 的边 上的高为 .

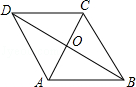
如图,平行四边形 ABCD的对角线 AC, BD相交于点 O,请你添加一个适当的条件 使其成为菱形(只填一个即可).
如图,将两张对边平行且等宽的纸条交叉叠放在一起,则重合部分构成的四边形 菱形(填“是”或“不是”
.

在矩形中,
,
,
,
分别为边
,
,
,
上的点(不与端点重合),对于任意矩形
,下面四个结论中,
①存在无数个四边形是平行四边形;
②存在无数个四边形是矩形;
③存在无数个四边形是菱形;
④至少存在一个四边形是正方形.
所有正确结论的序号是 .