初中数学勾股数试题

阅读：能够成为直角三角形三条边长的三个正整数 $a$， $b$， $c$，称为勾股数．世界上第一次给出勾股数通解公式的是我国古代数学著作《九章算术》，其勾股数组公式为： $\left\{\begin{array}{c}a=\frac{1}{2}(m^2-n^2)\\ b=\mathit{mn}\\ c=\frac{1}{2}(m^2+n^2).\end{array}\right.$其中 $m>n>0$， $m$， $n$是互质的奇数．

应用：当 $n=1$时，求有一边长为5的直角三角形的另外两条边长．

已知：整式，整式．

尝试 化简整式．

发现，求整式．

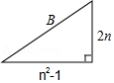
联想 由上可知，，当时，，，为直角三角形的三边长，如图．填写下表中的值：

直角三角形三边
勾股数组Ⅰ		8	17
勾股数组Ⅱ	35

阅读理解：如果一个正整数 $m$ 能表示为两个正整数 $a$ ， $b$ 的平方和，即 $m=a^2+b^2$ ，那么称 $m$ 为广义勾股数，则下面的四个结论：①7不是广义勾股数；②13是广义勾股数；③两个广义勾股数的和是广义勾股数；④两个广义勾股数的积是广义勾股数．依次正确的是 $($ 　　 $)$

A．

②④

B．

①②④

C．

①②

D．

①④