初中数学等腰三角形的性质填空题

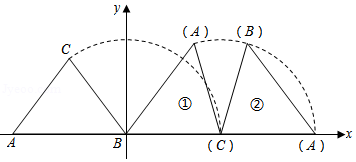
等腰三角形 $\mathit{ABC}$ 在平面直角坐标系中的位置如图所示，已知点 $A(-6,0)$ ，点 $B$ 在原点， $\mathit{CA}=\mathit{CB}=5$ ，把等腰三角形 $\mathit{ABC}$ 沿 $x$ 轴正半轴作无滑动顺时针翻转，第一次翻转到位置①，第二次翻转到位置② $\dots$ 依此规律，第15次翻转后点 $C$ 的横坐标是 　         　．

等腰三角形 $\mathit{ABC}$中，顶角 $A$为 $40°$，点 $P$在以 $A$为圆心， $\mathit{BC}$长为半径的圆上，且 $\mathit{BP}=\mathit{BA}$，则 $\angle \mathit{PBC}$的度数为　　．

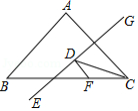
如图，若 $\mathit{\Delta ABC}$内一点 $P$满足 $\angle \mathit{PAC}=\angle \mathit{PCB}=\angle \mathit{PBA}$，则称点 $P$为 $\mathit{\Delta ABC}$的布罗卡尔点，三角形的布罗卡尔点是法国数学家和数学教育家克雷尔首次发现，后来被数学爱好者法国军官布罗卡尔重新发现，并用他的名字命名，布罗卡尔点的再次发现，引发了研究“三角形几何”的热潮．已知 $\mathit{\Delta ABC}$中， $\mathit{CA}=\mathit{CB}$， $\angle \mathit{ACB}=120°$， $P$为 $\mathit{\Delta ABC}$的布罗卡尔点，若 $\mathit{PA}=\sqrt{3}$，则 $\mathit{PB}+\mathit{PC}=$　　．

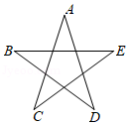
为庆祝中国共产党建党100周年，某校用红色灯带制作了一个如图所示的正五角星 $(A$ ， $B$ ， $C$ ， $D$ ， $E$ 是正五角星的五个顶点），则图中 $\angle A$ 的度数是 　　度．

如图，在矩形 $\mathit{ABCD}$中， $\mathit{AD}=5$， $\mathit{AB}=3$，点 $E$从点 $A$出发，以每秒2个单位长度的速度沿 $\mathit{AD}$向点 $D$运动，同时点 $F$从点 $C$出发，以每秒1个单位长度的速度沿 $\mathit{CB}$向点 $B$运动，当点 $E$到达点 $D$时，点 $E$， $F$同时停止运动．连接 $\mathit{BE}$， $\mathit{EF}$，设点 $E$运动的时间为 $t$，若 $\mathit{\Delta BEF}$是以 $\mathit{BE}$为底的等腰三角形，则 $t$的值为　　．

如图，已知在 $\mathit{\Delta ABC}$中， $\mathit{AB}=\mathit{AC}$．以 $\mathit{AB}$为直径作半圆 $O$，交 $\mathit{BC}$于点 $D$．若 $\angle \mathit{BAC}=40°$，则 $\stackrel{̂}{\mathit{AD}}$的度数是　　度．

若等腰三角形的顶角为 $120°$，腰长为 $2\mathit{cm}$，则它的底边长为　     　 $\mathit{cm}$．

在等腰 $\mathit{\Delta ABC}$中， $\mathit{AB}=\mathit{AC}$， $\angle B=50°$，则 $\angle A$的大小为　 　．

已知一个等腰三角形的两边长分别为2和4，则该等腰三角形的周长是　　．

如图，等腰 $\mathit{\Delta ABC}$的底边 $\mathit{BC}=20$，面积为120，点 $F$在边 $\mathit{BC}$上，且 $\mathit{BF}=3\mathit{FC}$， $\mathit{EG}$是腰 $\mathit{AC}$的垂直平分线，若点 $D$在 $\mathit{EG}$上运动，则 $\mathit{\Delta CDF}$周长的最小值为　　．

如图，在 $\mathit{\Delta ABC}$ 中， $\angle \mathit{ACB}=90°$ ， $\mathit{AC}<\mathit{BC}$ ．分别以点 $A$ ， $B$ 为圆心，大于 $\frac{1}{2}\mathit{AB}$ 的长为半径画弧，两弧交于 $D$ ， $E$ 两点，直线 $\mathit{DE}$ 交 $\mathit{BC}$ 于点 $F$ ，连接 $\mathit{AF}$ ．以点 $A$ 为圆心， $\mathit{AF}$ 为半径画弧，交 $\mathit{BC}$ 延长线于点 $H$ ，连接 $\mathit{AH}$ ．若 $\mathit{BC}=3$ ，则 $\mathit{\Delta AFH}$ 的周长为 　　．

如图，在正五边形 $\mathit{ABCDE}$ 中，连结 $\mathit{AC}$ ， $\mathit{BD}$ 交于点 $F$ ，则 $\angle \mathit{AFB}$ 的度数为 　　．

如图， $\mathit{\Delta ABC}$ 中， $\mathit{AB}=\mathit{AC}=2$ ， $P$ 是 $\mathit{BC}$ 上任意一点， $\mathit{PE}\perp \mathit{AB}$ 于点 $E$ ， $\mathit{PF}\perp \mathit{AC}$ 于点 $F$ ，若 $S_{\mathit{\Delta ABC}}=1$ ，则 $\mathit{PE}+\mathit{PF}=$ 　　．

如图， $\mathit{AB}$是 $\odot O$的弦，点 $C$在过点 $B$的切线上，且 $\mathit{OC}\perp \mathit{OA}$， $\mathit{OC}$交 $\mathit{AB}$于点 $P$，已知 $\angle \mathit{OAB}=22°$，则 $\angle \mathit{OCB}=$　　．

如图， $A$， $B$， $C$是 $\odot O$上的三个点， $\angle \mathit{AOB}=50°$， $\angle B=55°$，则 $\angle A$的度数为　　．