如图,在 中, ,矩形 的顶点 、 在 上,点 、 分别在 、 上,若 , ,且 ,则 的长为 .

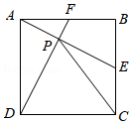
如图,已知 、 分别是正方形 的边 与 的中点, 与 交于 .则下列结论成立的是
| A. |
|
B. |
|
| C. |
|
D. |
|
数学活动--求重叠部分的面积.
问题情境:数学活动课上,老师出示了一个问题:
如图1,将两块全等的直角三角形纸片△ABC和△DEF叠放在一起,其中∠ACB=∠E=90°,BC=DE=6,AC=FE=8,顶点D与边AB的中点重合.
(1)若DE经过点C,DF交AC于点G,求重叠部分(△DCG)的面积;
(2)合作交流:“希望”小组受问题(1)的启发,将△DEF绕点D旋转,使DE⊥AB交AC于点H,DF交AC于点G,如图2,求重叠部分(△DGH)的面积.
如图,在△ABC中,∠C=90°,AC=BC=2 ,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE、DF、EF.在此运动变化的过程中,下列结论:
,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE、DF、EF.在此运动变化的过程中,下列结论:
①△DFE是等腰直角三角形;
②四边形CEDF的周长不变;
③点C到线段EF的最大距离为1.
其中正确的结论有__________(填写所有正确结论的序号)