如图,矩形 的对角线 , 交于点 , , ,过点 作 ,交 于点 ,过点 作 ,垂足为 ,则 的值为

| A. |
|
B. |
|
C. |
|
D. |
|
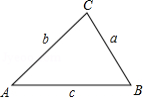
古希腊几何学家海伦和我国宋代数学家秦九韶都曾提出利用三角形的三边求面积的公式,称为海伦 秦九韶公式:如果一个三角形的三边长分别是 , , ,记 ,那么三角形的面积为 .如图,在 中, , , 所对的边分别记为 , , ,若 , , ,则 的面积为
| A. |
|
B. |
|
C. |
18 |
D. |
|
如图,正比例函数 与反比例函数 的图象相交于 、 两点,过点 作 轴的垂线交 轴于点 ,连接 ,则 的面积等于

| A. |
8 |
B. |
6 |
C. |
4 |
D. |
2 |
如图,在正方形 的对角线 上取一点 .使得 ,连接 并延长 到 ,使 , 与 相交于点 ,若 ,有下列结论:① ;② ;③ ;④ .则其中正确的结论有

| A. |
①②③ |
B. |
①②③④ |
C. |
①②④ |
D. |
①③④ |
正方形 的边 上有一动点 ,以 为边作矩形 ,且边 过点 .在点 从点 移动到点 的过程中,矩形 的面积

| A. |
先变大后变小 |
B. |
先变小后变大 |
C. |
一直变大 |
D. |
保持不变 |
如图,已知在四边形 中, , 平分 , , , ,则四边形 的面积是

| A. |
24 |
B. |
30 |
C. |
36 |
D. |
42 |
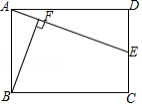
如图,在矩形 中, , .若点 是边 的中点,连接 ,过点 作 交 于点 ,则 的长为
| A. |
|
B. |
|
C. |
|
D. |
|
如图是一个等边三角形木框,甲虫 在边框
在边框 上爬行(
上爬行( ,
, 端点除外),设甲虫
端点除外),设甲虫 到另外两边的距离之和为
到另外两边的距离之和为 ,等边三角形
,等边三角形 的高为
的高为 ,则
,则 与
与 的大小关系是( )
的大小关系是( )

A. |
B. |
C. |
D.无法确定 |
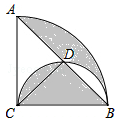
(年青海省西宁市)如图,在半径为2,圆心角为90°的扇形内,以BC为直径作半圆交AB于点D,连接CD,则阴影部分的面积是( )
A.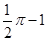 |
B.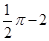 |
C.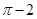 |
D.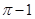 |