初中数学三角形选择题

如图，已知AB是⊙O的直径，∠AOE=60°，点C是AB延长线上一点，CE交⊙O于点D，且CD=OB，则∠C等于（  ）

A．10°

B．15°

C．20°

D．30°

如图，有一块直角三角形纸片，两直角边AC=6cm，BC=8cm．现将直角边AC沿直线AD折叠，使它落在斜边AB上，且与AE重合，则CD等于（ ）

A．2cm

B．3cm

C．4cm

D．5cm

如图A、B 、C三个居民小区的位置成三角形，现决定三个小区之间修建一个超市，使它到三个小区的距离相等，则超市应建在（   ）

A．AC、BC的两条高线的交点处      
B．∠A、∠B两内角平分线的交点处
C．AC、BC两边中线的交点处         
D．AC、BC两条边垂直平分线的交点处

已知P是△ABC内一点，连接PA，PB，PC，且PA=PB=PC，则P点一定是（     ）

A．△ABC的三条中线的交点

B．△ABC的三条内角平分线的交点

C．△ABC的三条高的交点

D．△ABC的三边的中垂线的交点

如图，在CD上求一点P，使它到OA，OB的距离相等，则P点是（  ）

A．线段CD的中点	B．OA与OB的中垂线的交点
C．OA与CD的中垂线的交点	D．CD与∠AOB的平分线的交点

如图，OP平分∠ AOB，PD⊥ OA于点D，点Q是射线OB上一个动点，若PD=2，则PQ的最小值为（ ）

A．PQ＜2

B．PQ=2

C．PQ＞2

D．以上情况都有可能

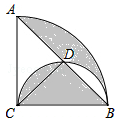
（年青海省西宁市）如图，在半径为2，圆心角为90°的扇形内，以BC为直径作半圆交AB于点D，连接CD，则阴影部分的面积是（ ）

A．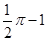

B．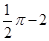

C．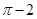

D．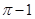

（年贵州省黔东南州）如图，四边形ABCD是菱形，AC=8，DB=6，DH⊥AB于H，则DH=（ ）

A．

B．

C．12

D．24

（年贵州省铜仁市）如图，在矩形ABCD中，BC=6，CD=3，将△BCD沿对角线BD翻折，点C落在点C¹处，BC¹交AD于点E，则线段DE的长为（ ）

A．3

B．

C．5

D．

（年贵州省毕节）如图，在△ABC中，∠C=90°，∠B=30°，AD平分∠CAB，交BC于点D，若CD=1，则BD=             ．

（年新疆乌鲁木齐市）等腰三角形的一个外角是60°，则它的顶角的度数是            ．

（年贵州省毕节）如图，在△ABC中，∠C=90°，∠B=30°，AD平分∠CAB，交BC于点D，若CD=1，则BD=             ．

（年贵州省毕节）等腰△ABC的底角为72°，腰AB的垂直平分线交另一腰AC于点E，垂足为D，连接BE，则∠EBC的度数为        ．

（年贵州省铜仁市）如图，∠ACB=9O°，D为AB中点，连接DC并延长到点E，使CE=CD，过点B作BF∥DE交AE的延长线于点F．若BF=10，则AB的长为      ．

（年云南省）如图，在△ABC中，BC=1，点P₁，M₁分别是AB，AC边的中点，点P₂，M₂分别是AP₁，AM₁的中点，点P₃，M₃分别是AP₂，AM₂的中点，按这样的规律下去，P_nM_n的长为     （n为正整数）．