初中数学三角形选择题

如图，∠BAC=∠DAF=90°，AB=AC，AD=AF，点D、E为BC边上的两点，且∠DAE=45°，连接EF、BF，则下列结论：①△AED≌△AEF ②△ABE∽△ACD，③BE＋DC＞DE④BE²＋DC²=DE²，其中正确的有（  ）个

A．1           B．2            C．3        D．4

如图，边长为2的正方形ABCD的顶点A在y轴上，顶点D在反比例函数y＝（x＞0）的图像上，已知点B的坐标是（，），则k的值为（   ）

A．10

B．8

C．6

D．4

如图， 中，，．点O是BC中点，点D沿B→A→C方向从B运动到C．设点D经过的路径长为，长为．则函数的图象大致为（  ）

如图，O是等边△ABC内一点，OA=3，OB=4，OC=5，将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′，下列结论：

①△BO′A可以由△BOC绕点B逆时针旋转60°得到；
②点O与O′的距离为4；
③∠AOB=150°；
④四边形AO BO′的面积为；
⑤．
其中正确的结论是（   ）

A．①②③

B．①②③④

C．①②③⑤

D．①②③④⑤

有以下条件：①一锐角与一边对应相等；②两边对应相等；③两锐角对应相等．其中能判断两直角三角形全等的是（  ）

A．①

B．②

C．③

D．①②

如图为八个全等的正六边形（六条边相等，六个角相等）紧密排列在同一平面上的情形．根据图中标示的各点位置，下列三角形中与△ACD全等的是（  ）

A．△ACF

B．△AED

C．△ABC

D．△BCF

如图，已知AB=AC，∠A=36°，AB的中垂线MD交AC于点D，交AB于点M．下列结论：①BD是∠ABC的平分线；②△BCD是等腰三角形；③DC+BC=AB，正确的有（  ）

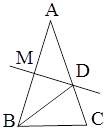
A．3个

B．2个

C．1个

D．0个

如图，圆柱底面半径为cm，高为9cm，点A、B分别是圆柱两底面圆周上的点，且A、B在同一母线上，用一根棉线从A点顺着圆柱侧面绕3圈到B点，则这根棉线的长度最短为（  ）

A．12cm               B．cm              C．15cm           D．cm

如图是一个等边三角形木框，甲虫在边框上爬行（，端点除外），设甲虫到另外两边的距离之和为，等边三角形的高为，则与的大小关系是（  ）

A．

B．

C．

D．无法确定

两组邻边分别相等的四边形叫做“筝形”，如图，四边形ABCD是一个筝形，其中AD=CD，AB=CB，小明在探究筝形的性质时，得到如下结论：

①AC⊥BD；②AO=CO=AC；③△ABD≌△CBD，其中正确的结论有（  ）

A．①②

B．①③

C．②③

D．①②③

如图，在△ABC中，∠ACB=90°，分别以点A和B为圆心，以相同的长（大于AB）为半径作弧，两弧相交于点M和N，作直线MN交AB于点D，交BC于点E，连接CD，下列结论错误的是（  ）

A．AD=BD             B．CD=BD
C．∠A=∠BED         D．∠ECD=∠EDC

如图，△ABC≌△DEF，点B、E、C、F在同一直线上，BF=7cm，EC=3cm，则BE长为（  ）

A．1cm            B．2cm            C．3cm           D．4cm

如图，等腰，，，于点，点是延长线上一点，点是线段上一点，，下面结论：
①；
②是等边三角形；
③；
④．
其中正确的是（  ）

A．②③

B．①②④

C．③④

D．①②③④

一个三角形的两个内角分别为55°和65°，这个三角形的外角不可能是（  ）

A．115°

B．120°

C．125°

D．130°

如图，在半圆的直径上作4个正三角形，如这半圆周长为C₁，这4个正三角形的周长和为C₂，则C₁和C₂的大小关系是（  ）

A．C1＞C2

B．C1＜C2

C．C1=C2

D．不能确定