初中数学余角和补角解答题

如图，直线AB与CD相交于点O，OD平分∠BOE，OF⊥OD
（1）∠AOF与∠EOF相等吗？
（2）写出图中和∠DOE互补的角．
（3）若∠BOE=60⁰，求∠AOD和∠EOF的度数．

如图，已知∠1+∠D=90°，BE∥FC，且DF⊥BE与点G，并分别于AB、CD交于点F、D，求证：AB∥CD．

如图，已知A、O、B三点在同一条直线上，OD平分∠AOC，OE平分∠BOC．

（1）若∠BOC=62°，求∠DOE的度数；
（2）若∠BOC=a°，求∠DOE的度数；
（3）图中是否有互余的角？若有请写出所有互余的角．

如图，点O是直线AB、CD的交点，∠AOE=∠COF=90°．如果∠EOF=32°，求∠AOD的度数．

如图，O为直线AB上一点，∠AOC=50°，OD平分∠AOC，∠DOE=90°

（1）求出∠BOD的度数；
（2）请通过计算说明OE是否平分∠BOC．

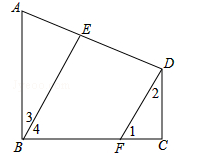
（本题6分）AB⊥BC，∠1+∠2=90°，∠2=∠3．BE与DF平行吗？为什么？
解：BE∥DF．
∵AB⊥BC，
∴∠ABC=      °，
即∠3+∠4=      °．
又∵∠1+∠2=90°，
且∠2=∠3，
∴       =       ．
理由是：________________．
∴BE∥DF．
理由是：________________．