初中数学二次函数综合题填空题

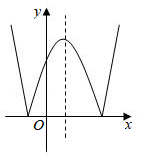
我们定义一种新函数：形如 $y=|a{x}^2+\mathit{bx}+c|(a\ne 0,b^2-4\mathit{ac}>0)$的函数叫做“鹊桥”函数．小丽同学画出了“鹊桥”函数 $y=|x^2-2x-3|$的图象（如图所示），并写出下列五个结论：①图象与坐标轴的交点为 $(-1,0)$， $(3,0)$和 $(0,3)$；②图象具有对称性，对称轴是直线 $x=1$；③当 $-1⩽x⩽1$或 $x⩾3$时，函数值 $y$随 $x$值的增大而增大；④当 $x=-1$或 $x=3$时，函数的最小值是0；⑤当 $x=1$时，函数的最大值是4．其中正确结论的个数是　　．

直线 y＝ kx+ b与抛物线 $y=\frac{1}{4}{x}^2$ 交于 A（ x ₁， y ₁）、 B（ x ₂， y ₂）两点，当 OA⊥ OB时，直线 AB恒过一个定点，该定点坐标为 　　．

已知函数 $y=\left\{\begin{array}{c}-x^2+2x(x>0)\\ -x(x⩽0)\end{array}\right.$的图象如图所示，若直线 $y=x+m$与该图象恰有三个不同的交点，则 $m$的取值范围为　　．

如图，抛物线 $y=-x^2+2x+m+1(m$为常数）交 $y$轴于点 $A$，与 $x$轴的一个交点在2和3之间，顶点为 $B$．

①抛物线 $y=-x^2+2x+m+1$与直线 $y=m+2$有且只有一个交点；

②若点 $M(-2,y_1)$、点 $N(\frac{1}{2}$， $y_2)$、点 $P(2,y_3)$在该函数图象上，则 $y_1<y_2<y_3$；

③将该抛物线向左平移2个单位，再向下平移2个单位，所得抛物线解析式为 $y=-{(x+1)}^2+m$；

④点 $A$关于直线 $x=1$的对称点为 $C$，点 $D$、 $E$分别在 $x$轴和 $y$轴上，当 $m=1$时，四边形 $\mathit{BCDE}$周长的最小值为 $\sqrt{34}+\sqrt{2}$．

其中正确判断的序号是　　．

如图，在平面直角坐标系xOy中，点O是边长为2的正方形ABCD的中心．写出一个函数，使它的图象与正方形ABCD有公共点，这个函数的表达式为 ．