在平面直角坐标系中,设二次函数 , , 是实数, .
(1)若函数 的对称轴为直线 ,且函数 的图象经过点 ,求函数 的表达式.
(2)若函数 的图象经过点 ,其中 ,求证:函数 的图象经过点 , .
(3)设函数 和函数 的最小值分别为 和 ,若 ,求 , 的值.
已知二次函数图象的顶点坐标为
,该二次函数图象的对称轴与
轴的交点为
,
是这个二次函数图象上的点,
是原点.
(1)不等式是否成立?请说明理由;
(2)设是
的面积,求满足
的所有点
的坐标.
若x1、x2是关于一元二次方程ax2+bx+c(a≠0)的两个根,则方程的两个根x1、x2和系数a、b、c有如下关系:x1+x2=- ,x1•x2=
,x1•x2=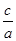 .把它称为一元二次方程根与系数关系定理.如果设二次函数y=ax2+bx+c(a≠0)的图象与x轴的两个交点为A(x1,0),B(x2,0).利用根与系数关系定理可以得到A、B两个交点间的距离为:AB=|x1-x2|=
.把它称为一元二次方程根与系数关系定理.如果设二次函数y=ax2+bx+c(a≠0)的图象与x轴的两个交点为A(x1,0),B(x2,0).利用根与系数关系定理可以得到A、B两个交点间的距离为:AB=|x1-x2|=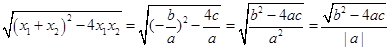 ;
;
参考以上定理和结论,解答下列问题:
设二次函数y=ax2+bx+c(a>0)的图象与x轴的两个交点A(x1,0),B(x2,0),抛物线的顶点为C,显然△ABC为等腰三角形.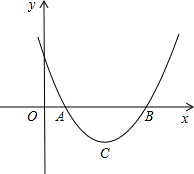
(1)当△ABC为直角三角形时,求b2-4ac的值;
(2)当△ABC为等边三角形时,求b2-4ac的值.
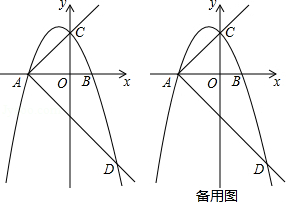
如图,抛物线 与 轴交于点 和 ,与 轴交于点 .
(1)求抛物线的表达式;
(2)作射线 ,将射线 绕点 顺时针旋转 交抛物线于另一点 ,在射线 上是否存在一点 ,使 的周长最小.若存在,求出点 的坐标;若不存在,请说明理由;
(3)在(2)的条件下,点 为抛物线的顶点,点 为射线 上的一个动点,且点 的横坐标为 ,过点 作 轴的垂线 ,垂足为 ,点 从点 出发沿 方向运动,直线 随之运动,当 时,直线 将四边形 分割成左右两部分,设在直线 左侧部分的面积为 ,求 关于 的函数表达式.