数形结合是解决数学问题常用的思想方法.如图,直线 和直线 相交于点 ,根据图象可知,方程 的解是
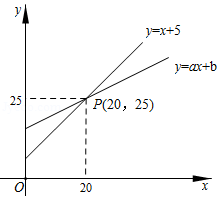
A. B. C. D.
在平面直角坐标系中, 为坐标原点.若直线 分别与 轴、直线 交于点 、 ,则 的面积为
A.2B.3C.4D.6
如图,已知函数 和 图象交于点 ,当 时,根据图象可得 的取值范围是
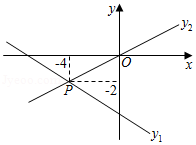
A. B. C. D.
对于实数 , ,定义符号 , ,其意义为:当 时, , ;当 时, , .例如: , ,若关于 的函数 , ,则该函数的最大值为
A. B.1C. D.
如图,正比例函数 是常数, 的图象与一次函数 的图象相交于点 ,点 的纵坐标是2,则不等式 的解集是
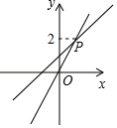
A. B. C. D.
如图,在平面直角坐标系中,直线 l 1: y=﹣ x+1与 x轴, y轴分别交于点 A和点 B,直线 l 2: y= kx( k≠0)与直线 l 1在第一象限交于点 C.若∠ BOC=∠ BCO,则 k的值为( )
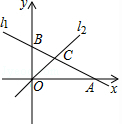
| A. |
|
B. |
|
C. |
|
D. |
2 |
已知直线l1:y=﹣3x+b与直线l2:y=﹣kx+m在同一坐标系中的图象交于点(1,﹣2),那么方程组 的解是( )
A. B. C. D.
如图,在 中, , ,点 在边 上,且 ,点 为 的中点,点 为边 上的动点,当点 在 上移动时,使四边形 周长最小的点 的坐标为

| A. |
|
B. |
, |
C. |
, |
D. |
|
如图,在平面直角坐标系中,直线 与直线 交于点 ,过 作 轴的垂线,垂足为 ,过 作 的平行线交 于 ,过 作 轴的垂线,垂足为 ,过 作 的平行线交 于 ,过 作 轴的垂线,垂足为 按此规律,则点 的纵坐标为

| A. |
|
B. |
|
C. |
|
D. |
|