初中数学两点间的距离公式解答题

探究：小明在求同一坐标轴上两点间的距离时发现，对于平面直角坐标系内任意两点 $P_1(x_1$， $y_1)$， $P_2(x_2$， $y_2)$，可通过构造直角三角形利用图1得到结论： $P_1{P}_2=\sqrt{{(x_2-x_1)}^2+{(y_2-y_1)}^2}$他还利用图2证明了线段 $P_1{P}_2$的中点 $P(x,y)P$的坐标公式： $x=\frac{x_1+x_2}{2}$， $y=\frac{y_1+y_2}{2}$．

（1）请你帮小明写出中点坐标公式的证明过程；

运用：（2）①已知点 $M(2,-1)$， $N(-3,5)$，则线段 $\mathit{MN}$长度为　　；

②直接写出以点 $A(2,2)$， $B(-2,0)$， $C(3,-1)$， $D$为顶点的平行四边形顶点 $D$的坐标：　　；

拓展：（3）如图3，点 $P(2,n)$在函数 $y=\frac{4}{3}x(x⩾0)$的图象 $\mathit{OL}$与 $x$轴正半轴夹角的平分线上，请在 $\mathit{OL}$、 $x$轴上分别找出点 $E$、 $F$，使 $\mathit{\Delta PEF}$的周长最小，简要叙述作图方法，并求出周长的最小值．

数和形是数学的两个主要研究对象，我们经常运用数形结合、数形转化的方法解决一些数学问题．下面我们来探究“由数思形，以形助数”的方法在解决代数问题中的应用．

探究一：求不等式 $|x-1|<2$的解集

（1）探究 $|x-1|$的几何意义

如图①，在以 $O$为原点的数轴上，设点 $A\text{'}$对应的数是 $x-1$，由绝对值的定义可知，点 $A\text{'}$与点 $O$的距离为 $|x-1|$，可记为 $A\text{'}O=|x-1|$．将线段 $A\text{'}O$向右平移1个单位得到线段 $\mathit{AB}$，此时点 $A$对应的数是 $x$，点 $B$对应的数是1．因为 $\mathit{AB}=A\text{'}O$，所以 $\mathit{AB}=|x-1|$．因此， $|x-1|$的几何意义可以理解为数轴上 $x$所对应的点 $A$与1所对应的点 $B$之间的距离 $\mathit{AB}$．

（2）求方程 $|x-1|=2$的解

因为数轴上3和 $-1$所对应的点与1所对应的点之间的距离都为2，所以方程的解为3， $-1$．

（3）求不等式 $|x-1|<2$的解集

因为 $|x-1|$表示数轴上 $x$所对应的点与1所对应的点之间的距离，所以求不等式解集就转化为求这个距离小于2的点对应的数 $x$的范围．

请在图②的数轴上表示 $|x-1|<2$的解集，并写出这个解集．

探究二：探究 $\sqrt{{(x-a)}^2+{(y-b)}^2}$的几何意义

（1）探究 $\sqrt{x^2+y^2}$的几何意义

如图③，在直角坐标系中，设点 $M$的坐标为 $(x,y)$，过 $M$作 $\mathit{MP}\perp x$轴于 $P$，作 $\mathit{MQ}\perp y$轴于 $Q$，则 $P$点坐标为 $(x,0)$， $Q$点坐标为 $(0,y)$， $\mathit{OP}=\left|x\right|$， $\mathit{OQ}=\left|y\right|$，在 $\text{Rt}\Delta \text{OPM}$中， $\mathit{PM}=\mathit{OQ}=\left|y\right|$，则 $\mathit{MO}=\sqrt{O{P}^2+P{M}^2}=\sqrt{|x{|}^2+|y{|}^2}=\sqrt{x^2+y^2}$，因此， $\sqrt{x^2+y^2}$ 的几何意义可以理解为点 $M(x,y)$与点 $O(0,0)$之间的距离 $\mathit{MO}$．

（2）探究 $\sqrt{{(x-1)}^2+{(y-5)}^2}$的几何意义

如图④，在直角坐标系中，设点 $A\text{'}$的坐标为 $(x-1,y-5)$，由探究二（1）可知， $A\text{'}O=\sqrt{{(x-1)}^2+{(y-5)}^2}$，将线段 $A\text{'}O$先向右平移1个单位，再向上平移5个单位，得到线段 $\mathit{AB}$，此时点 $A$的坐标为 $(x,y)$，点 $B$的坐标为 $(1,5)$，因为 $\mathit{AB}=A\text{'}O$，所以 $\mathit{AB}=\sqrt{{(x-1)}^2+{(y-5)}^2}$，因此 $\sqrt{{(x-1)}^2+{(y-5)}^2}$的几何意义可以理解为点 $A(x,y)$与点 $B(1,5)$之间的距离 $\mathit{AB}$．

（3）探究 $\sqrt{{(x+3)}^2+{(y-4)}^2}$的几何意义

请仿照探究二（2）的方法，在图⑤中画出图形，并写出探究过程．

（4） $\sqrt{{(x-a)}^2+{(y-b)}^2}$的几何意义可以理解为：　　．

拓展应用：

（1） $\sqrt{{(x-2)}^2+{(y+1)}^2}+\sqrt{{(x+1)}^2+{(y+5)}^2}$的几何意义可以理解为：点 $A(x,y)$与点 $E(2,-1)$的距离和点 $A(x,y)$与点 $F$　　（填写坐标）的距离之和．

（2） $\sqrt{{(x-2)}^2+{(y+1)}^2}+\sqrt{{(x+1)}^2+{(y+5)}^2}$的最小值为　　（直接写出结果）

特例感知

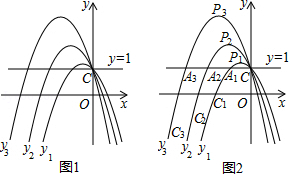
（1）如图1，对于抛物线，，，下列结论正确的序号是　　；

①抛物线，，都经过点；

②抛物线，的对称轴由抛物线的对称轴依次向左平移个单位得到；

③抛物线，，与直线的交点中，相邻两点之间的距离相等．

形成概念

（2）把满足为正整数）的抛物线称为“系列平移抛物线”．

知识应用

在（2）中，如图2．

①“系列平移抛物线”的顶点依次为，，，，，用含的代数式表示顶点的坐标，并写出该顶点纵坐标与横坐标之间的关系式；

②“系列平移抛物线”存在“系列整数点（横、纵坐标均为整数的点）”：，，，，，其横坐标分别为，，，，为正整数），判断相邻两点之间的距离是否都相等，若相等，直接写出相邻两点之间的距离；若不相等，说明理由．

③在②中，直线分别交“系列平移抛物线”于点，，，，，连接，，判断，是否平行？并说明理由．