已知关于的一元二次方程
.
(1)求证:无论为任何实数,此方程总有两个实数根;
(2)若方程的两个实数根为、
,满足
,求
的值;
(3)若的斜边为5,另外两条边的长恰好是方程的两个根
、
,求
的内切圆半径.
已知关于的一元二次方程
有两不相等的实数根.
①求的取值范围.
②设,
是方程的两根且
,求
的值.
已知一元二次方程 的两个根为 , ,下列结论正确的是
| A. |
|
B. |
|
| C. |
, 都是有理数 |
D. |
, 都是正数 |
已知关于的一元二次方程
.
(1)求证:对于任意实数,方程总有两个不相等的实数根;
(2)设方程的两个实数根分别为,
,当
时,求
的值.
若x1、x2是关于一元二次方程ax2+bx+c(a≠0)的两个根,则方程的两个根x1、x2和系数a、b、c有如下关系:x1+x2=- ,x1•x2=
,x1•x2=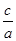 .把它称为一元二次方程根与系数关系定理.如果设二次函数y=ax2+bx+c(a≠0)的图象与x轴的两个交点为A(x1,0),B(x2,0).利用根与系数关系定理可以得到A、B两个交点间的距离为:AB=|x1-x2|=
.把它称为一元二次方程根与系数关系定理.如果设二次函数y=ax2+bx+c(a≠0)的图象与x轴的两个交点为A(x1,0),B(x2,0).利用根与系数关系定理可以得到A、B两个交点间的距离为:AB=|x1-x2|=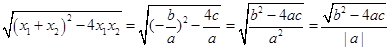 ;
;
参考以上定理和结论,解答下列问题:
设二次函数y=ax2+bx+c(a>0)的图象与x轴的两个交点A(x1,0),B(x2,0),抛物线的顶点为C,显然△ABC为等腰三角形.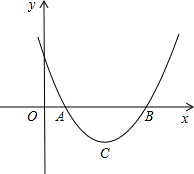
(1)当△ABC为直角三角形时,求b2-4ac的值;
(2)当△ABC为等边三角形时,求b2-4ac的值.
若关于x的一元二次方程x2+bx+c=0的两个实数根分别为x1=﹣2,x2=4,则b+c的值是( )
| A.﹣10 | B.10 | C.﹣6 | D.﹣1 |
(年江西省南昌市)已知一元二次方程 的两根为m,n,则
的两根为m,n,则 = .
= .
(年青海省西宁市)若矩形的长和宽是方程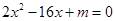 (0<m≤32)的两根,则矩形的周长为 .
(0<m≤32)的两根,则矩形的周长为 .
(年云南省曲靖市)一元二次方程 有两个不相等的实数根且两根之积为正数,若c是整数,则c= .(只需填一个).
有两个不相等的实数根且两根之积为正数,若c是整数,则c= .(只需填一个).
(年贵州省黔东南州)设 ,
, 是一元二次方程
是一元二次方程 的两根,则
的两根,则 =( )
=( )
| A.6 | B.8 | C.10 | D.12 |
(年蒙自市初中学业水平第一次模拟测试)已知 、
、 是一元二次方程
是一元二次方程 的两个根,则
的两个根,则 等于( )
等于( )
A. |
B. |
C. |
D. |