初中数学一元二次方程选择题

小刚在解关于 $x$ 的方程 $a{x}^2+\mathit{bx}+c=0(a\ne 0)$ 时，只抄对了 $a=1$ ， $b=4$ ，解出其中一个根是 $x=-1$ ．他核对时发现所抄的 $c$ 比原方程的 $c$ 值小2．则原方程的根的情况是 $($ 　　 $)$

A．	不存在实数根	B．	有两个不相等的实数根
C．	有一个根是 $x=-1$	D．	有两个相等的实数根

设 $\alpha$ 、 $\beta$ 是一元二次方程 $x^2+2x-1=0$ 的两个根，则 $\mathit{\alpha \beta }$ 的值是 $($ 　　 $)$

A．

2

B．

1

C．

$-2$

D．

$-1$

$a$ ， $b$ ， $c$ 为常数，且 ${(a-c)}^2>a^2+c^2$ ，则关于 $x$ 的方程 $a{x}^2+\mathit{bx}+c=0$ 根的情况是 $($ 　　 $)$

A．

有两个相等的实数根

B．

有两个不相等的实数根

C．

无实数根

D．

有一根为0

一种药品原价每盒25元，经过两次降价后每盒16元．设两次降价的百分率都为 $x$ ，则 $x$ 满足 $($ 　　 $)$

A．

$16(1+2x)=25$

B．

$25(1-2x)=16$

C．

$16{(1+x)}^2=25$

D．

$25{(1-x)}^2=16$

已知实数m，n满足m﹣n²=2，则代数式m²+2n²+4m﹣1的最小值等于（ ）

A．﹣14

B．﹣6

C．8

D．11

若关于x的一元二次方程x²+bx+c=0的两个实数根分别为x₁=﹣2，x₂=4，则b+c的值是（  ）

A．﹣10

B．10

C．﹣6

D．﹣1

若n（n≠0）是关于x的方程x²+mx+2n=0的根，则m+n的值为（  ）

A．1

B．2

C．﹣1

D．﹣2

某城市2011年已有绿化面积100公顷，经过两年绿化，绿化面积逐年增加，到2013底增加到144公顷，设绿化面积平均每年的增长率为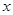，则根据题意可列方程为（  ）

A．

B．

C．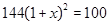

D．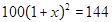

（年贵州省黔东南州）设，是一元二次方程的两根，则=（ ）

A．6

B．8

C．10

D．12

（年贵州省毕节）若关于x的一元二次方程+（2k﹣1）x+﹣1=0有实数根，则k的取值范围是（ ）

A．k≥

B．k＞

C．k＜

D．k≤

（年贵州省铜仁市）已知关于x的一元二次方程3x²+4x﹣5=0，下列说法不正确的是（ ）

A．方程有两个相等的实数根	B．方程有两个不相等的实数根
C．没有实数根	D．无法确定

（年云南省）下列一元二次方程中，没有实数根的是（ ）

A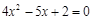．	B．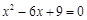
C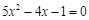．	D．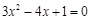

（年蒙自市初中学业水平第一次模拟测试）已知、是一元二次方程的两个根，则等于（  ）

A．

B．

C．

D．

一个盒子里有完全相同的三个小球，球上分别标有数字。随机摸出一个小球（不放回）其数字记为p ，再随机摸出另一个小球其数字记为q ，则满足关于的方程有实数根的概率是（  ）

A．

B．

C．

D．

关于x的方程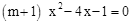有实数根，则的取值范围是（   ）

A．>–5	B．≥–5且≠–1
C．>–5且≠–1	D．≥–5