用标有1克，2克，6克的砝码各一个，在一架无刻度的天平上称量重物．如果天平两端均可放置砝码，那么可以称出的不同克数的重量共有多少种?
学习有理数得乘法后，老师给同学们这样一道题目：计算：49
×（-5），看谁算的又快又对，有两位同学的解法如下：
小明：原式=-
×5=-
=-249
；
小军：原式=（49+）×（-5）=49×（-5）+×（-5）=-249；
（1）对于以上两种解法，你认为谁的解法较好？
（2）上面的解法对你有何启发，你认为还有更好的方法吗？如果有，请把它写出来；
（3）用你认为最合适的方法计算：19
×（-8）
某出租车从停车场出发，沿着东西向的大街行驶，到晚上6时，一天的行驶记录如下：（向东行驶记为正，向西行驶记为负，单位：千米）－4、＋7、－9、＋8、＋6、－4、－3、＋12
（1）到晚上6时，出租车在什么位置？
（2）若汽车每千米耗油0.2升，则从停车场出发到晚上6时，出租车共耗油多少升？
同样大小的黑色棋子按如图所示的规律摆放：
（1）第5个图形有多少颗黑色棋子？
（2）第2014个图形有多少颗棋子？请说明理由．
（本题10分）某出租车一天下午以
地为出发地在东西方向运营，向东走为正，向西走为负，行车里程（单位：
）依先后顺序记录如下：
，
，
，
，
，
，，
，
，
．将最后一名乘客送到目的地，出租车离地多远？在地的什么方向？若每千米的价格为
元，司机一个下午的营业额是多少？
有一种“二十四点”的游戏，其游戏规则是这样的：任取四个1至13之间的自然数，将这四个数（每个数用且只用一次）进行加减乘除四则运算，使其结果等于24．例如对1，2，3，4可作运算：（1+2+3）×4=24．[注意上述运算与4×（2+3+1）应视为相同方法的运算]．现有四个有理数3，4，﹣6，10，运用上述规则写出三种不同方法的运算式，使其结果等于24，运算式如下：
（1） ；
（2） ；
（3） ．
初一年级举行篮球循环赛，规则是：胜一场得2分，平一场得0分，负一场得﹣2分，比赛结果是初一（3）班2胜1平4负，问该班最后得分是多少？
某班抽查了10名同学的期末成绩，以80分为基准，超出的记为正数，不足的记为负数，记录的结果如下：
+8，-3，+12，-7，-10，-3，-8，+1，0，+10．
（1）这10名同学中最高分是多少？最低分是多少？
（2）10名同学中，低于80分的所占的百分比是多少？
（3）10名同学的平均成绩是多少？
某股民上星期五买进某公司股票1000股，每股25元，下表为本周内每日该股票的涨跌情况：（单价：元）
| 星期 |
一 |
二 |
三 |
四 |
五 |
| 每股涨跌 （与前一天比较） |
+2 |
－0．5 |
＋1．5 |
–1．8 |
+0．8 |
（1）星期三收盘时，每股是多少元？
（2）本周内最高价是每股多少元？最低价是每股多少元？
（3）已知该股民买进股票时付了0．15%的手续费，卖出时需付成交额0．15%的手续费和0．1%的交易税，如果他一直观望到星期五才将股票全部卖出，请算算他本周的收益如何？
甲、乙两辆汽车分别从A、B两地同时相向而行．已知甲车行完全程需要8小时，乙车行完全程需要6小时，如果两车各行3小时，两车之间的距离占全程的几分之几？如果两车各行4小时，两车之间的距离占全程的几分之几？
有理数a、b、c在数轴上的位置如图：
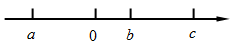
（1）判断正负，用“＞”或“＜”填空：b－c 0，a＋b 0，c－a 0；
（2）化简：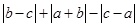
．
（本题8分）定义新运算。
，如
，计算下列各式。
（1）
（2）
，其中
．
粤公网安备 44130202000953号