初中数学整式的加减填空题

分解因式：2x²-8=             ．

已知2a+2b+ab=，且a+b+3ab=，那么a+b+ab的值  ．

分解因式：a³b-2a²b²+ab³=                 ．

如果x²-2（m+1）x+4是一个完全平方公式，则m=             ．

分解因式：a³﹣9a=         ．

（本题8分）从1开始，连续的奇数相加，它们和的情况如下表：

加数的个数n	连 续 奇 数 的 和 S
1	1=1
2	1＋3＝4[21]
3	1＋3＋5＝9[:21]
4	1＋3＋5＋7＝16
5	1＋3＋5＋7＋9＝25

 
（1）如果n=11时，那么S的值为________；
（2）猜想：用n的代数式表示S的公式为S=1+3+5+7+…+2n－1=_________  ；
（3）根据上题的规律计算1001+1003+1005+…+2009+2011的值（要有计算过程）．

如果m，n是两个不相等的实数，且满足m²-m=3，n²-n=3，那么代数式2n²-mn+2m+2015=          ．

分解因式：（2a-b）²+8ab=          ．

分解因式：xy²﹣2xy+x=__________．

因式分解：x³﹣4x=___________．

若a²-b²=，a-b=，则a+b的值为          .

若a=2，a+b=3，则a²+ab=           .

分解因式：﹣4a=         ．

已知，则的值为      ．

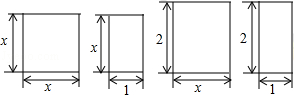
把下面四个图形拼成一个大长方形，并据此写出一个多项式的因式分解            ．