如图,在 中,顶点 , , ,将 与正方形 组成的图形绕点 顺时针旋转,每次旋转 ,则第70次旋转结束时,点 的坐标为

| A. |
|
B. |
|
C. |
|
D. |
|
下列图形都是由同样大小的五角星按一定的规律组成,其中第①个图形一共有2个五角星,第②个图形一共有8个五角星,第③个图形一共有18个五角星,…,则第⑥个图形中五角星的个数为( )

| A.50 | B.64 | C.68 | D.72 |
用●表示实圆,用○表示空心圆,现有若干个实圆与空心圆按一定规律排列如下:●○●●○●●●○●○●●○●●●○●○●●○●●●○……问:前2011个圆中,有________个空心圆.
| A.670 | B.668 | C.669 | D.671 |
如图,小红作出了边长为1的第1个正△A1B1C1,算出了正△A1B1C1的面积,然后分别取△A1B1C1三边的中点A2,B2,C2,作出了第2个正△A2B2C2,算出了正△A2B2C2的面积,用同样的方法,作出了第3个正△A3B3C3,算出了正△A3B3C3的面积…,由此可得,第2014个正△A2014B2014C2014的面积是( )

A. |
B. |
C. |
D. |
如图,一只青蛙在圆周上标有数字的五个点上跳,若它停在奇数点上,则下次沿顺时针方向跳三个点;若停在偶数点上,则下次沿逆时针方向跳一个点.若青蛙从5这点开始跳,则经过2015次后它停在哪个数对应的点上( )

| A.1 | B.3 | C.4 | D.5 |
如图,在平面直角坐标系中,已知点A(1,1),B(﹣1,1),C(﹣1,﹣2),D(1,﹣2),动点P从点A出发,以每秒2个单位的速度按逆时针方向沿四边形ABCD的边做环绕运动;另一动点Q从点C出发,以每秒3个单位的速度按顺时针方向沿四边形CBAD的边做环绕运动,则第2014次相遇点的坐标是( )

| A.(﹣1,﹣1) | B.(﹣1,1) | C.(﹣2,2) | D.(1,2) |
观察下列一组图形中点的个数,其中第1个图中共有4个点,第2个图中共有10个点,第3个图中共有19个点,…按此规律第8个图中共有点的个数是( )

| A.109 | B.85 | C.72 | D.66 |
图①是一块边长为1,周长记为 的正三角形(三边相等的三角形)纸板,沿图①的底边剪去一块边长为
的正三角形(三边相等的三角形)纸板,沿图①的底边剪去一块边长为 的正三角形纸板后得到图②,然后沿同一底边依次剪去一块更小的正三角形纸板(即其边长为前一块被剪掉正三角形纸板边长的
的正三角形纸板后得到图②,然后沿同一底边依次剪去一块更小的正三角形纸板(即其边长为前一块被剪掉正三角形纸板边长的 )后,得图③,④,…,记第n(n
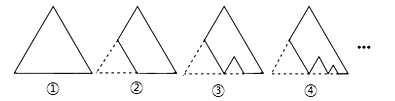
)后,得图③,④,…,记第n(n 3)块纸板的周长为
3)块纸板的周长为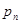 ,则
,则 的值为( )
的值为( )
A. |
B. |
C.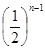 |
D. |
等边△ABC在数轴上的位置如图所示,点A、C对应的数分别为0和﹣1,若△ABC绕着顶点顺时针方向在数轴上连续翻转,翻转1次后,点B所对应的数为1;则翻转2012次后,点B所对应的数是( )

A.2013 B.2010 C.2011 D.2012
古希腊人常用小石子在沙滩上摆成各种形状来研究数,例如:他们研究过图1中的1,3,6,10,…,由于这些数能够表示成三角形,将其称为三角形数;类似地,称图2中的1,4,9,16,…,这样的数为正方形数.下列数中既是三角形数又是正方形数的是( )

| A.15 | B.25 | C.55 | D.1225 |
电子跳蚤游戏盘是如图所示的△ABC,AB=6,AC=7,BC=8.如果跳蚤开始时在BC边的P0处,BP0=2.跳蚤第一步从P0跳到AC边的P1(第1次落点)处,且CP1=CP0;第二步从P1跳到AB边的P2(第2次落点)处,且AP2=AP1;第三步从P2跳到BC边的P3(第3次落点)处,且BP3=BP2;…;跳蚤按上述规则一直跳下去,第n次落点为Pn(n为正整数),则点P2007与P2010之间的距离为( )

| A.1 | B.2 | C.3 | D.4 |
如图,用火柴棍拼成一排由三角形组成的图形,如果图形中含有16个三角形,则需要( )根火柴棍.

| A.30根 | B.31根 | C.32根 | D.33根 |
一质点P从距原点1个单位的M点处向原点方向跳动,第一次跳动到OM的中点M1处,第二次从M1跳到OM1的中点M2处,第三次从点M2跳到OM2的中点M3处,如此不断跳动下去,则第n次跳动后,该质点到原点O的距离为( )
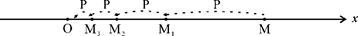
A.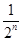 |
B.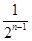 |
C.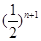 |
D.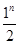 |
由点组成的正方形,每条边上的点数n与总点数之间的关系如图所示,则当n=60时,计算 s的值为( )

| A.220 | B.236 | C.240 | D.216 |