规律探究.下面有8个算式,排成4行2列
2+2, 2×2
3+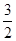 , 3×
, 3×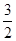
4+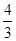 , 4×
, 4×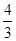
5+ , 5×
, 5× ……, ……
……, ……
(1)同一行中两个算式的结果怎样?
(2)算式2005+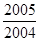 和2005×
和2005×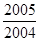 的结果相等吗?
的结果相等吗?
(3)请你试写出算式,试一试,再探索其规律,并用含自然数n的代数式表示这一规律.
观察下列顺序排列的等式:9 0+1=1,9
0+1=1,9 1+2=11,9
1+2=11,9 2+3=21,9
2+3=21,9 3+4=31,9
3+4=31,9 +5=41,……
+5=41,……
根据以上所反映的规律,猜想,第n个等式(n为正整数)应为( )
| A.9(n-1)+n=10(n-1)+1 |
| B.9n+n=(n-1)+n |
| C.9n+(n-1)=n2 -1 |
| D.9n+n=10n+1 |
如图,将1~2025这2025个自然数按图中规律分别排列在网格中,除对角线AB经过的45个数外,其它的数被分成两部分,对角线AB右上方的990个数之和记为S1,对角线AB左下方的990个数之和记为S2.则S1﹣S2= .

观察下列各式:
1×2= (1×2×3−0×1×2),
(1×2×3−0×1×2),
2×3= (2×3×4−1×2×3),
(2×3×4−1×2×3),
3×4= (3×4×5−2×3×4),…
(3×4×5−2×3×4),…
计算:3×(1×2+2×3+3×4+…+99×100)=( )
| A.97×98×99 | B.98×99×100 |
| C.99×100×101 | D.100×101×102 |
给出依次排列的一列数:
—1、2、—4、8、—16、32,---------
(1)按照给出的这个数列的某种规律,继续写出后面的3项: , , ;
(2)这一列数第n个数是什么?
让我们轻松一下,做一个数字游戏:
第一步:取一个自然数 ,计算
,计算 得
得 ;
;
第二步:算出 的各位数字之和得
的各位数字之和得 ,计算
,计算 得
得 ;
;
第三步,算出 的各位数字之和得
的各位数字之和得 ,计算
,计算 得
得 ;
;
…………
以此类推,则 .
.
定义一种新运算:观察下列各式:1⊙3=1×4+3=7 ;3⊙(-1)= 3×4-1=11;5⊙4="5×4+4=24" ;4⊙(-3)= 4×4-3=13
(1)请你想一想:用代数式表示a⊙b的结果为:___________;
(2)若a≠b,那么a⊙b______b⊙a(填入“=”或“≠ ”);
(3)若a⊙(-2b)= 4,请计算(a-b)⊙(2a+b)的值.
定义:a是不为1的有理数,我们把 称为a的差倒数,如:2的差倒数是
称为a的差倒数,如:2的差倒数是 ,-1的差倒数是
,-1的差倒数是 .已知a1=
.已知a1= ,a2是a1的差倒数,a3是a2的差倒数,a4是a3的差倒数,…,依此类推,则a2014=_______.
,a2是a1的差倒数,a3是a2的差倒数,a4是a3的差倒数,…,依此类推,则a2014=_______.