某市为了节约用水，对自来水的收费标准作如下规定：每月每户用水不超过10吨的部分，按2元/吨收费；超过10吨的部分按2．5元/吨收费．
（1）若黄老师家5月份用水16吨，问应交水费多少元？
（2）若黄老师家7月用水a吨，问应交水费多少元？（用a的代数式表示）
某市区自2014年1月起，居民生活用水开始实行阶梯式计量水价，该阶梯式计量水价分为三级（如下表所示）：
| 月用水量（吨） |
水价（元/吨） |
| 第一级 20吨以下（含20吨） |
1．6 |
| 第二级 20吨﹣30吨（含30吨） |
2．4 |
| 第三级 30吨以上 |
3．2 |
例：某用户的月用水量为32吨，按三级计量应缴水费为：
1．6×20＋2．4×10＋3．2×2＝62．4（元）
（1）如果甲用户的月用水量为12吨，则甲需缴的水费为 元；
（2）如果乙用户缴的水费为39．2元，则乙月用水量 吨；
（3）如果丙用户的月用水量为a吨，则丙用户该月应缴水费多少元？（用含a的代数式表示，并化简）
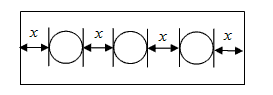
为了做一个试管架，在长为a（cm）（a﹥6）的木板上钻3个小孔（如图），每个小孔的直径为2cm，则x等于（ ）．
A． |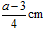
B． |
C． |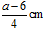
D． |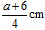
今年弟弟10岁，姐姐12岁,经过t年后,姐弟年龄之和为（ ）．
| A．（12+t）岁 | B．（11+t）岁 | C．（22+2t）岁 | D．（22+t）岁 |
如图，每个图案都由若干个棋子摆成，依照此规律，第n个图案中棋子的总个数可以用含n的代数式表示为 ．
某商场销售一种西装和领带，西装每套定价1000元，领带每条定价200元．“国庆节”
期间商场决定开展促销活动，活动期间向客户提供两种优惠方案．
方案一：买一套西装送一条领带；
方案二：西装和领带都按定价的90%付款．
现某客户要到该商场购买西装20套，领带x条（x＞20）．
（1）若该客户按方案一购买，需付款 元．（用含x的代数式表示）
若该客户按方案二购买，需付款 元．（用含x的代数式表示）
（2）若x=30，通过计算说明此时按（1）哪种方案购买较为合算？
（3）当x=30时，你能给出一种更为省钱的购买方案吗？试写出你的购买方法．
如图，长方形的长为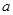
，宽为
，
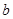（1）用含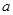、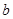的代数式表示右图阴影部分的面积S阴影．
（2）当a=5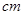
，b=2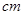时，求S阴影．（
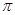取3．14）
一个矩形的周长为30，若矩形的一边长用字母
表示，则此矩形的面积为（ ）
A． |
B． |
C． |
D． |
如图，平面内有公共端点的6条射线O
| A．O | B．O | C．O | D．OE、OF，按照图中的规律，从射线OA开始，按照逆时针方向，依次在射线上画点表示1，2，3，4，5，6，7，… |
（1）根据图中规律，表示“19”的点在射线 上；
（2）按照图中规律推算，表示“2014”的点在射线 上；
（3）请你写出在射线OC上表示的数的规律（用含
的代数式表示） ．
全班同学排成长方形长队，每排的同学数为a，排数比每排同学数的3倍还多2，那么全班同学数是（ ）
A． |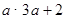
B． |
C． |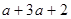
D． |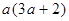
，宽比长少3，则长方形周长L=________．
元，加上20％的利润后优惠8％出售，则售出价为（ ）
的2倍与
的
的和”用代数式表示为 ．
粤公网安备 44130202000953号