如图,船A、B在东西方向的海岸线MN上,均收到已触礁搁浅的船P的求救信号,已知船P在船A的北偏东60°方向上,在船B的北偏西37°方向上,AP=30海里.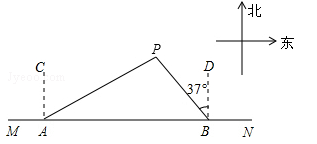
(1)尺规作图:过点P作AB所在直线的垂线,垂足为E(要求:保留作图痕迹,不写作法);
(2)求船P到海岸线MN的距离(即PE的长);
(3)若船A、船B分别以20海里/时、15海里/时的速度同时出发,匀速直线前往救援,试通过计算判断哪艘船先到达船P处.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
有一轮船在A处测得南偏东30°方向上有一小岛P,轮船沿正南方向航行至B处,测得小岛P在南偏东45°方向上,按原方向再航行10海里至C处,测得小岛P在正东方向上,则A,B之间的距离是( )海里.
A. |
B. |
C.10 | D.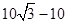 |
小明从家出发,外出散步,到一个公共阅报栏前看了一会报后,继续散步了一段时间,然后回家,如图描述了小明在散步过程汇总离家的距离s(米)与散步所用时间t之间的函数关系,根据图象,下列信息错误的是( )
| A.小明看报用时8分钟 |
| B.公共阅报栏距小明家200米 |
| C.小明离家最远的距离为400米 |
| D.小明从出发到回家共用时16分钟 |
如图所示的函数图象反映的过程是:小明从家去书店看一会儿书,又去学校取封信后马上回家,其中x表示时间(单位:小时),y表示小明离家的距离(单位:千米),则小明从学校回家的平均速度为 千米∕小时.
九(1)班同学在上学期的社会实践活动中,对学校旁边的山坡护墙和旗杆进行了测量.
(1)如图1,第一小组用一根木条CD斜靠在护墙上,使得DB与CB的长度相等,如果测量得到∠CDB=38°,求护墙与地面的倾斜角α的度数.
(2)如图2,第二小组用皮尺量的EF为16米(E为护墙上的端点),EF的中点离地面FB的高度为1.9米,请你求出E点离地面FB的高度.
(3)如图3,第三小组利用第一、第二小组的结果,来测量护墙上旗杆的高度,在点P测得旗杆顶端A的仰角为45°,向前走4米到达Q点,测得A的仰角为60°,求旗杆AE的高度(精确到0.1米).
备用数据:tan60°=1.732,tan30°=0.577, =1.732,
=1.732, =1.414.
=1.414.
如图,在同一平面内,两条平行高速公路l1和l2间有一条“Z”型道路连通,其中AB段与高速公路l1成30°角,长为20km;BC段与AB、CD段都垂直,长为10km,CD段长为30km,求两高速公路间的距离(结果保留根号).
在△ABC中,AB=5,BC=6,B为锐角且sinB=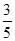 ,则∠C的正弦值等于( )
,则∠C的正弦值等于( )
A. |
B. |
C. |
D. |
已知:如图,小明在打网球时,要使球恰好能打过而且落在离网5米的位置上(网球运行轨迹为直线),则球拍击球的高度h应为( )
| A.0.9m | B.1.8m | C.2.7m | D.6m |