初中数学计算器—基础知识填空题

已知点P（-3，4）,关于x轴对称的点的坐标为            。

如图，在平面直角坐标系xOy中，矩形AOCD的顶点A的坐标是（0，4），现有两动点P，Q，点P从点O出发沿线段OC（不包括端点O，C）以每秒2个单位长度的速度匀速向点C运动，点Q从点C出发沿线段CD（不包括端点C，D）以每秒1个单位长度的速度匀速向点D运动．点P，Q同时出发，同时停止，设运动时间为t（秒），当t=2（秒）时，PQ=2．

（1）求点D的坐标，并直接写出t的取值范围；
（2）连接AQ并延长交x轴于点E，把AE沿AD翻折交CD延长线于点F，连接EF，则△AEF的面积S是否随t的变化而变化？若变化，求出S与t的函数关系式；若不变化，求出S的值；
（3）在（2）的条件下，t为何值时，四边形APQF是梯形？

如图，点A在反比例函数 （）的图象上，AB⊥y轴于点B，点C在x轴正半轴上，且OC=2AB，点E在线段AC上，且AE=3EC，点D为OB的中点，若△ADE的面积为6，则k的值为        ．

下图反映了某地某天气温的变化情况，如A点表示早晨8时的气温为15度，记作(8，15)。结合图形完成下列问题：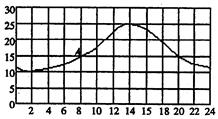

（1）20时的气温为      度，记作          ；
（2）(2，10)的实际意义是                     ；
（3）说出这一天中何时气温最高? 并表示出来。

在平面直角坐标系中，规定把一个点先绕原点逆时针旋转45°，再作出旋转后的点关于原点的对称点称为一次变换.已知点A的坐标为（－1，0），把点A经过连续2013次这样的变换得到的点A₂₀₁₃的坐标是    ．

函数中自变量x的取值范围是    ．

已知AB在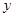轴上，A点的坐标为（0，-3），并且AB＝7，则B的坐标为             。

点关于轴对称的点的坐标是     ；点关于原点对称的点的坐标是     ．

若点M（a-2，2a+3）是x轴上的点，则a的值是           。

设点M（1,2）关于原点的对称点为M′，则M′的坐标为        .

如图，在梯形ABCD中，AD//BC，AB=DC，AC与BD相交于点P。已知A(2, 3)，B(1, 1)，D(4, 3)，则点P的坐标为（       ，       ）。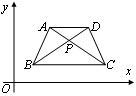

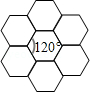
在函数y= 中，自变量x的取值范围是         ．

如图，蜂巢的横截面由正六边形组成，且能无限无缝隙拼接，称横截面图形由全等正多边形组成，且能无限无缝隙拼接的多边形具有同形结构．
若已知具有同形结构的正 $n$边形的每个内角度数为 $\alpha$，满足： $360=k\alpha$（ $k$为正整数），多边形外角和为360°，则 $k$关于边数n的函数是 $n$（写出 $n$的取值范围）

如图，是经过某种变换后得到的图形.如果中任意一点
的坐标为（，），那么它的对应点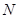的坐标为                 .