洛伦兹力演示仪是由励磁线圈(也叫亥姆霍兹线圈)、洛伦兹力管和电源控制部分组成的。励磁线圈是一对彼此平行的共轴串联的圆形线圈,它能够在两线圈之间产生匀强磁场。洛伦兹力管的圆球形玻璃泡内有电子枪,能够连续发射出电子,电子在玻璃泡内运动时,可以显示出电子运动的径迹。其结构如图所示。
(1)给励磁线圈通电,电子枪垂直磁场方向向左发射电子,恰好形成如“结构示意图”所示的圆形径迹,则励磁线圈中的电流方向是顺时针方向还是逆时针方向?
(2)两个励磁线圈中每一线圈为N = 140匝,半径为R =" 140" mm,两线圈内的电流方向一致,大小相同为I = 1.00A,线圈之间距离正好等于圆形线圈的半径,在玻璃泡的区域内产生的磁场为匀强磁场,其磁感应强度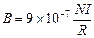 (特斯拉)。灯丝发出的电子经过加速电压为U=125V的电场加速后,垂直磁场方向进入匀强磁场区域,通过标尺测得圆形径迹的直径为D = 80.0mm,请估算电子的比荷
(特斯拉)。灯丝发出的电子经过加速电压为U=125V的电场加速后,垂直磁场方向进入匀强磁场区域,通过标尺测得圆形径迹的直径为D = 80.0mm,请估算电子的比荷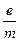 。(答案保留2位有效数字)
。(答案保留2位有效数字)
(3)为了使电子流的圆形径迹的半径增大,可以采取哪些办法?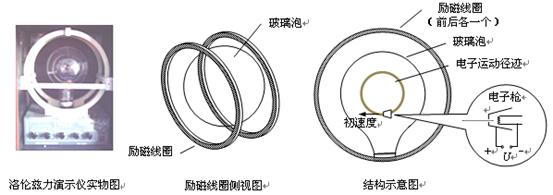
两个板长均为L的平板电极,平行正对放置,相距为d,极板之间的电势差为U,板间电场可以认为是均匀的。一个α粒子从正极板边缘以某一初速度垂直于电场方向射入两极板之间,到达负极板时恰好落在极板边缘。已知质子电荷为e,质子和中子的质量均视为m,忽略重力和空气阻力的影响,求:
(1)极板间的电场强度E;
(2)α粒子的初速度v0。
如图所示,在质量为M=0.99kg的小车上,固定着一个质量为m=10g、电阻R=1W的矩形单匝线圈MNPQ,其中MN边水平,NP边竖直,高度l=0.05m。小车载着线圈在光滑水平面上一起以v0=10m/s的速度做匀速运动,随后进入一水平有界匀强磁场(磁场宽度大于小车长度),完全穿出磁场时小车速度v1=2m/s。磁场方向与线圈平面垂直并指向纸内、磁感应强度大小B=1.0T。已知线圈与小车之间绝缘,小车长度与线圈MN边长度相同。求:
(1)小车刚进入磁场时线圈中感应电流I的大小和方向;
(2)小车通过磁场的过程中线圈电阻的发热量Q;
(3)小车进入磁场过程中线圈克服安培力所做的功W。
两个带电量均为+q小球,质量均为m,固定在轻质绝缘直角框架OAB(框架的直角边长均为L)的两个端点A、B上,另一端点用光滑铰链固定在O点,整个装置可以绕垂直于纸面的水平轴在竖直平面内自由转动。
(1)若施加竖直向上的匀强电场E1,使框架OA边水平、OB边竖直并保持静止状态,则电场强度E1多大?
(2)若改变匀强电场的大小和方向(电场仍与框架面平行),为使框架的OA边水平、OB边竖直(B在O的正下方),则所需施加的匀强电场的场强E2至少多大?方向如何?
(3)若框架处在匀强电场E1中OA边水平、OB边竖直并保持静止状态时,对小球B施加一水平向右的恒力F,则小球B在何处时速度最大?最大值是多少?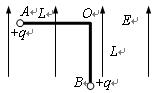
一个“┌”型细玻璃管A、B两端开口,水平段内有一段长为5cm的水银柱,初始时长度数据如图所示。现将玻璃管B端封闭,然后将下端A插入大水银槽中,整个过程温度不变,稳定后竖直管内水银面比大水银槽面低5cm,已知大气压强为75cmHg。求:
(1)稳定后玻璃管B端水平段内被封闭气体的压强为多少?
(2)竖直管A端插入水银槽的深度h。
某研究性学习小组用加速度传感器探究物体从静止开始做直线运动的规律,得到了质量为1.0kg的物体运动的加速度随时间变化的关系图线,如图所示。
(1)请简要说明物体的运动情况;
(2)估算物体在t=10.0s时的速度大小;
(3)估算从t=10.0s到t=12.0s的时间内合外力对物体做的功。
(共18分)如图所示,一个质量为m,带电量为+q的微粒,从a点以大小为v0的初速度竖直向上射入水平方向的匀强电场中。微粒通过最高点b时的速度大小为2v0方向水平向右。求:
(1)该匀强电场的场强大小E;
(2)a、b两点间的电势差Uab;
(3)该微粒从a点到b点过程中速率的最小值vmin。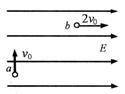
(共18分)如图所示,在一光滑的长直轨道上,放着若干完全相同的小木块,每个小木块的质量均为m,且体积足够小均能够看成质点,其编号依次为0、1、2、……n……,相邻各木块之间的距离分别记作: 。在所有木块都静止的初始条件下,有一个沿轨道方向水平向右的恒力F持续作用在0号小木块上,使其与后面的木块连接发生碰撞,假如所有碰撞都是完全非弹性的(碰后合为一体共速运动)。求:
。在所有木块都静止的初始条件下,有一个沿轨道方向水平向右的恒力F持续作用在0号小木块上,使其与后面的木块连接发生碰撞,假如所有碰撞都是完全非弹性的(碰后合为一体共速运动)。求:
(1)在0号木块与1号木块碰撞后瞬间,其共同速度的表达式;
(2)若F=10牛,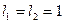 米,那么在2号木块被碰撞后的瞬间,系统的总动能为多少?
米,那么在2号木块被碰撞后的瞬间,系统的总动能为多少?
(3)在F=10牛,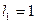 米的前提下,为了保持正在运动的物块系统在每次碰撞之前的瞬间其总动能都为一个恒定的数值,那么我们应该设计第
米的前提下,为了保持正在运动的物块系统在每次碰撞之前的瞬间其总动能都为一个恒定的数值,那么我们应该设计第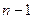 号和第n号木块之间距离
号和第n号木块之间距离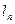 为多少米?
为多少米?
(共16分)如图所示,MN和PQ为竖直方向的两平行长直金属导轨,间距l为0.40m,电阻不计. 导轨所在平面与磁感庆强度B=5.0T的匀强磁场垂直。质量m=6.0×10-2kg、电阻r=0.5Ω的金属杆ab始终垂直于导轨,并与其保持光滑接触。导轨两端分别接有阻值均为3.0Ω的电阻R1和R2。重力加速度取10m/s2,且导轨足够长,若使金属杆ab从静止开始下滑,求:
(1)杆下滑的最大速率vm;
(2)稳定后整个电路耗电的总功率P;
(3)杆下滑速度稳定之后电阻R2两端的电压U.
如图所示,半径R=0.9 m的四分之一圆弧形光滑轨道竖直放置,圆弧最低点B与长为l=l m的水平面相切于B点,BC离地面高h=0.45 m,C点与一倾角为θ=30º的光滑斜面连接。质量m=1.0 kg的小滑块从圆弧顶点D由静止释放,已知滑块与水平面间的动摩擦因数μ=0.1,取g=10 m/s2。求:
(1)小滑块刚到达圆弧的B点时对圆弧的压力;
(2)小滑块从C点运动到地面所需的时间。
[物理——选修3-5]
(1)下列说法正确的是_____(填入选项前的字母,有填错的不得分)
A. 经过6次α衰变和4次β衰变后,成为稳定的原子核 经过6次α衰变和4次β衰变后,成为稳定的原子核 |
B.发现中子的核反应方程为 |
| C.γ射线一般伴随着α或β射线产生,在这三种射线中γ射线的穿透能力最强,电离能力也最强 |
| D.氢原子核外电子从半径较小的轨道跃迁到半径较大的轨道时,电子的动能减小,电势能增大,原子能量减小 |
(2)如图所示,一质量为M,长为l的长方形木板B放在光滑的水平地面上,在其右端放一质量为m的小木块 A(可视为质点),m<M。现以地面为参考系,给A和B以大小相等,方向相反的初速度,使A开始向左运动,B开始向右运动,但最后A刚好没有滑离B板。
A(可视为质点),m<M。现以地面为参考系,给A和B以大小相等,方向相反的初速度,使A开始向左运动,B开始向右运动,但最后A刚好没有滑离B板。
(i)若已知A和B的初速度大小为v0,求它们最后的速度大小和方向;
(ii)若初速度的大小未知,求小木块向左运动到达的最远处(从地面上看)离出发点的距离。
[物理——选修3-4]
(1)其振动系统的固有频率为f0,在周期性驱动力的作用下做受迫振动,驱动力的频率为f。若驱动力的振幅保持不变,下列说法正确的是 _____(填入选项前的字母,有填错的不得分)
| A.当f<f0时,该振动系统的振幅随f增大而减小 |
| B.当f>f0时,该振动系统的振幅随f减小而增大 |
| C.该振动系统的振动稳定后,振动的频率等于f0 |
| D.该振动系统的振动稳定后,振动的频率等于f |
(2)一棱镜的截面为直角三角形ABC,∠A=30º,斜边AB=a。棱镜材料的折射率为n= 。在此截面所在的平面内,一条光线以45º的入射角从AC边的中点M射入棱镜。画出光路图,并求光线从棱镜射出的点的位置(不考虑光线沿原路返回的情况)。
。在此截面所在的平面内,一条光线以45º的入射角从AC边的中点M射入棱镜。画出光路图,并求光线从棱镜射出的点的位置(不考虑光线沿原路返回的情况)。
[物理——选修3-3]
(1)带有活塞的气缸内封闭一定量的理想气体. 气体开始处于状态a,然后经过过程ab到达状态b或经过过程ac到达状态c,b、c状态温度相同,如V-T图所示. 设
气体在状态b和状态c的压强分别为pb和pc,在过程ab和ac中吸收的热量分别为Qab和Qac,则 _____(填入选项前的字母,有填错的不得分)
| A.pb>pc,Qab>Qac | B.pb>pc,Qab<Qac |
| C.pb<pc,Qab>Qac | D.pb<pc,Qab<Qac |
(2)图中系统由左右两个侧壁绝热、底部导热、截面均为S的容器组成。左容器足够高,上端敞开,右容器上端由导热材料封闭。两容器的下端由可忽略容积的细管连通。
容器内两个绝热的活塞A、B下方封有氮气,B上方封有氢气. 大气的压强为p0,温度为T0=273 K,两活塞因自身重量对下方气体产生的附加压强均为0.1 p0。系统平衡时,各气柱的高度如图所示。现将系统底部浸入恒温热水槽中,再次平衡时A上升了一定高度。用外力将A缓慢推回第一次平衡时的位置并固定,第三次达到平衡后,氢气柱高度为0.8 h。氮气和氢气均可视为理想气体。求:
(i)第二次平衡时氮气的体积;(ii)水的温度。
如图所示,一个质量为m、带电量为q的正离子,在D处沿着图中所示的方向进入磁感应强度为B的匀强磁场,此磁场方向垂直纸面向里,结果离子正好从离开A点距离为d的小孔C沿垂直于AC的方向进入匀强电场,此电场方向与AC平行且向上,最后离子打在B处,而B离A点距离为2d(AB⊥AC),不计粒子重力,离子运动轨迹始终在纸面内。求:
(1)离子从D到B所需的时间;
(2)离子到达B处时的动能。