如图,在竖直平面内由 圆弧 和 圆弧BC组成的光滑固定轨道,两者在最低点B平滑连接。 弧的半径为R, 弧的半径为 。一小球在A点正上方与A相距 处由静止开始自由下落,经A点沿圆弧轨道运动。
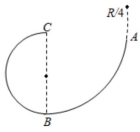
(1)求小球在B、A两点的动能之比;
(2)通过计算判断小球能否沿轨道运动到C点。
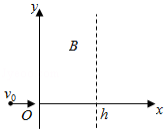
如图,在 , 区域中存在方向垂直于纸面的匀强磁场,磁感应强度 的大小可调,方向不变。一质量为 、电荷量为 的粒子以速度 从磁场区域左侧沿 轴进入磁场,不计重力。
(1)若粒子经磁场偏转后穿过 轴正半轴离开磁场,分析说明磁场的方向,并求在这种情况下磁感应强度的最小值 ;
(2)如果磁感应强度大小为 ,粒子将通过虚线所示边界上的一点离开磁场。求粒子在该点的运动方向与 轴正方向的夹角及该点到 轴的距离。
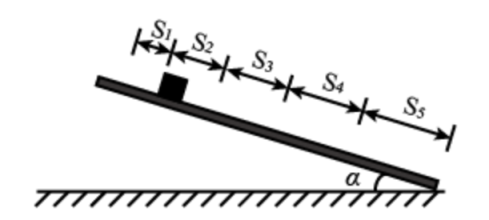
为测量小铜块与瓷砖表面间的动摩擦因数,一同学将贴有标尺的瓷砖的一端放在水平桌面上,形成一倾角为 α的斜面(已知sin α=0.34,cos α=0.94),小铜块可在斜面上加速下滑,如图所示。该同学用手机拍摄小铜块的下滑过程,然后解析视频记录的图像,获得5个连续相等时间间隔(每个时间间隔Δ T=0.20 s)内小铜块沿斜面下滑的距离 s i( i=1,2,3,4,5),如下表所示。
| s 1 |
s 2 |
s 3 |
s 4 |
s 5 |
| 5.87cn |
7.58cm |
9.31cm |
11.02cm |
12.74cm |
由表中数据可得,小铜块沿斜面下滑的加速度大小为_______m/s 2,小铜块与瓷砖表面间的动摩擦因数为_________。(结果均保留2位有效数字,重力加速度大小取9.80 m/s 2)
某型号质谱仪的工作原理如图甲所示。 、 为竖直放置的两金属板,两板间电压为 , 板为记录板,分界面 将 、 间区域分为宽度均为 的Ⅰ、Ⅱ两部分, 、 、 、 所在平面相互平行, 、 为 、 上两正对的小孔。以 、 所在直线为 轴,向右为正方向,取 轴与 板的交点 为坐标原点,以平行于 板水平向里为 轴正方向,竖直向上为 轴正方向,建立空间直角坐标系 .区域Ⅰ、Ⅱ内分别充满沿 轴正方向的匀强磁场和匀强电场,磁感应强度大小、电场强度大小分别为 和 .一质量为 ,电荷量为 的粒子,从 孔飘入电场(初速度视为零),经 孔进入磁场,过 面上的 点(图中未画出)进入电场,最终打到记录板 上。不计粒子重力。
(1)求粒子在磁场中做圆周运动的半径 以及 点到 轴的距离 ;
(2)求粒子打到记录板上位置的 坐标;
(3)求粒子打到记录板上位置的 坐标(用 、 表示);
(4)如图乙所示,在记录板上得到三个点 、 、 ,若这三个点是质子 、氚核 、氦核 的位置,请写出这三个点分别对应哪个粒子(不考虑粒子间的相互作用,不要求写出推导过程)。

如图所示,长为L、内壁光滑的直管与水平地面成30°角固定放置.将一质量为m的小球固定在管底,用一轻质光滑细线将小球与质量为M=km的小物块相连,小物块悬挂于管口.现将小球释放,一段时间后,小物块落地静止不动,小球继续向上运动,通过管口的转向装置后做平抛运动,小球在转向过程中速率不变.(重力加速度为g)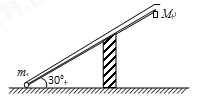
(1)求小物块下落过程中的加速度大小;
(2)求小球从管口抛出时的速度大小;
(3)试证明小球平抛运动的水平位移总小于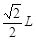
某地“欢乐谷”大型的游乐性主题公园,园内有一种大型游戏机叫“跳楼机”.让人体验短暂的“完全失重”,非常刺激.参加游戏的游客被安全带固定在座椅上,由电动机将座椅沿光滑的竖直轨道提升到离地面50m高处,然后由静止释放.为研究方便,认为人与座椅沿轨道做自由落体运动2s后,开始受到恒定阻力而立即做匀减速运动,且下落到离地面5m高处时速度刚好减小到零.然后再让座椅以相当缓慢的速度稳稳下落,将游客送回地面.(取g=10m/s2)
求:(1)座椅在自由下落结束时刻的速度是多大?
(2)在匀减速阶段,座椅对游客的作用力大小是游客体重的多少倍?
某战士在倾角为30o山坡上进行投掷手榴弹训练。他从A点以某一初速度v0沿水平方向投出手榴弹,正好落在B点,测得AB=90m。若空气阻力不计,(g=10m/s2)求: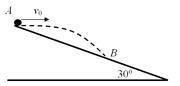
(1)手榴弹抛出的速度?
(2)从抛出开始经多长时间手榴弹与山坡间的距离最大?并求出此时手榴弹与山坡间的距离?
如图所示,质量为m的物体放在倾角为θ的粗糙斜面上,斜面固定在电梯中,物体和斜面保持相对静止。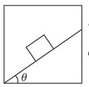
(1)若电梯匀速上升,求物块受到斜面的摩擦力和支持力是多少?
(2)若电梯以加速度a加速上升,求物块对斜面的摩擦力和压力是多少?
质量为2 kg的物体在水平推力F的作用下沿水平面做直线运动,一段时间后撤去F,其运动的v-t图象如图所示.g取10 m/s2,求:
(1)物体与水平面间的动摩擦因数μ;
(2)水平推力F的大小;
(3)0~10 s内物体运动位移的大小.
足够长的倾角θ=53°的斜面固定在水平地面上,一物体以v0=6.4 m/s的初速度从斜面底端向上滑行,该物体与斜面间的动摩擦因数μ=0.8,如图所示.(sin53°=0.8,cos53°=0.6,g取10 m/s2)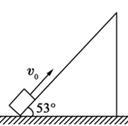
(1)求物体从开始到再次返回斜面底端所需的时间?
(2)求返回斜面底端时的速度?
如图所示,在倾角为θ的光滑斜面上有两个用轻质弹簧相连接的物块A、B,它们的质量相等,均为m,弹簧的劲度系数为k,C为一固定挡板。系统处于静止状态.现开始用沿斜面方向的力F(F未知)拉物块A使之向上做加速度为a的匀加速运动,当物块B刚要离开C时,沿斜面方向的力F(F未知)保持此时的值变为恒力,且此时弹簧与物块A连接处断裂,物块A在恒力作用下继续沿斜面向上运动.重力加速度为g,求: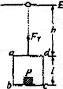
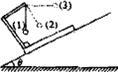
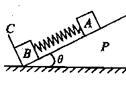
(1)恒力F的大小;
(2)物块A从断裂处继续前进相同的距离后的速度.
如图所示,一足够长的木板静止在水平面上,质量M=0.4kg,长木板与水平面间的动摩擦因数μ1=0.1,一质量m=0.4kg的小滑块以v0=1.8m/s的速度从长木板的右端滑上长木板,滑块与长木板间动摩擦因数μ2=0.4,小滑块可看成质点,重力加速度g取10m/s2,求:
(1)小滑块刚滑上长木板时,长木板的加速度大小a1和小滑块加速度大小a2;
(2)小滑块与长木板速度相等时,小滑块相对长木板上滑行的距离L;
(3)从小滑块滑上长木板到最后静止下来的过程中,小滑块运动的总距离S.
如图一可视为质点的物体,在倾角θ=30°的固定斜面上,向下轻轻一推,它恰好匀速下滑.已知斜面长度为L=5m.求:欲使物体由斜面底端开始,沿斜面冲到顶端,物体上滑时的初速度至少为多大?(g取10m/s2)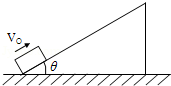
为了测量某住宅大楼每层的平均高度(层高)及电梯运行情况,甲、乙两位同学在一楼 电梯内用电子体重计及秒表进行了以下实验,甲同学站在体重计上,乙同学记录电梯从地面一楼到顶层全过程中,体重计示数随时间变化的情况,并作出了如图所示的图象.已知t=0时,电梯静止不动,从电梯内楼层按钮上获知该大楼共19层.求:
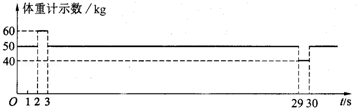
(1)电梯启动和制动时的加速度大小;
(2)该大楼的层高.