(9分)已知潜水员在岸上和海底吸入空气的密度分别为1.3 kg/m3和2.1 kg/m3,空气的摩尔质量为0.029 kg/mol,阿伏加德罗常数NA=6.02×1023 mol-1。若潜水员呼吸一次吸入2 L空气,试估算潜水员在海底比在岸上每呼吸一次多吸入空气的分子数。(结果保留1位有效数字)
1897年汤姆孙发现电子后,许多科学家为测量电子的电荷量做了大量的探索。1907~1916年密立根用带电油滴进行实验,发现油滴所带的电荷量是某一数值e的整数倍,于是称这数值e为基本电荷。
如图所示,完全相同的两块金属板正对着水平放置,板间距离为d。当质量为m的微小带电油滴在两板间运动时,所受空气阻力的大小与速度大小成正比。两板间不加电压时,可以观察到油滴竖直向下做匀速运动,通过某一段距离所用时间为t1;当两板间加电压U(上极板的电势高)时,可以观察到同一油滴竖直向上做匀速运动,且在时间t2内运动的距离与在时间t1内运动的距离相等。忽略空气浮力,重力加速度为g。
(1)判断上述油滴的电性,要求说明理由;
(2)求上述油滴所带的电荷量Q;
(3)在极板间照射X射线可以改变油滴的带电量。再采用上述方法测量油滴的电荷量。如此重复操作,测量出油滴的电荷量Qi,如下表所示。如果存在基本电荷,那么油滴所带的电荷量Qj应为某一最小单位的整数倍,油滴电荷量的最大公约数(或油滴带电量之差的最大公约数)即为基本电荷e。请根据现有数据求出基本电荷的电荷量e (保留3位有效数字)。
| 实验次序 |
1 |
2 |
3 |
4 |
5 |
| 电荷量Qi(10-18C) |
0.95 |
1.10 |
1.41 |
1.57 |
2.02 |
用油膜法可粗略测出阿伏加德罗常数,把密度ρ=0.8×103 kg/m3的某种油,用滴管滴出一滴油在水面上形成油膜,已知这滴油的体积V=0.5×10-3 cm3,形成的油膜的面积S="0.7" m2,油的摩尔质量Ml="0.09" kg/mol.若把油膜看成单分子层,每个油分子看成球形,那么:
(a)油分子的直径为多大?
(b)由以上数据可测出的阿伏加德罗常数大约为多少?(保留一位有效数字)
(1)已知某种气体的摩尔质量为M,密度为ρ,阿伏伽德罗常数为N。则该种气体中每个分子的质量为 ;分子的平均间距为 。
(2)如图甲所示,内径均匀、两端开口的U形管竖直放置,管中装入水银。稳定后,两管中水银面与管口的距离均为L=10cm。现将右侧管口密封,然后从左侧管口处将一活塞缓慢向下推入管中,直到左右两侧水银面高度差h=6cm时为止,如图乙所示。已知大气压强P0=75.8cmHg。求活塞在左管内竖直向下移动的距离。设管中气体温度不变。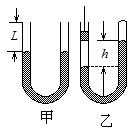
1 mol铜的质量为63.5 g,铜的密度是8.9×103 kg/m3,试计算(NA=6.02×1023 mol-1)
(1)一个铜原子的体积;
(2)假若铜原子为球形,求铜原子的直径;
(3)铜原子的质量.
已知金刚石的密度是ρ=3500kg/m3, 有一小块金刚石, 体积是V=6×10-8m3, 摩尔质量为M=12×10-3 kg/mol,阿伏伽德罗常数为NA= 6×1023/mol,求:
(1)这小块金刚石中含有多少个碳原子? (此问需数据计算)
(2)设想金刚石中碳原子是紧密地堆在一起的球体, 试估算碳原子的直径.(此问只需公式计算即可).
某同学做“用油膜法估测分子大小”的实验时,在边长约30cm的浅盘里倒入约2cm深的水,然后将痱子粉均匀的撒在水面上,用注射器滴一滴 (选填“纯油酸”、“油酸水溶液”或“油酸酒精溶液”)在水面上.稳定后,在玻璃板上描下油膜的轮廓,放到坐标纸上估算出油膜的面积.实验中若撒的痱子粉过多,则计算得到的油酸分子的直径偏 (选填“大”或“小”).
(1)在课本上粗测油酸分子的大小的实验中,油酸酒精溶液的浓度为每1000mL溶液中有纯油酸1mL,用注射器量得1mL上述溶液有200滴,把一滴该溶液滴入盛水的表面撒有痱子粉的浅盘里,待水面稳定后,测得油酸膜的近似轮廓如图所示,图中正方形小方格的边长为1cm,则每一滴油酸酒精溶液中含有纯油酸的体积是_______mL,油酸膜的面积是______cm2,根据上述数据,估测出油酸分子的直径是____ ____m。
(2)某同学在用油膜法估测分子直径实验中,计算结果明显偏大,可能是由于 。
| A.油酸未完全散开 |
| B.油酸中含有大量的酒精 |
| C.计算油膜面积时舍去了所有不足一格的方 |
| D.求每滴体积时,1mL的溶液的滴数多记了10滴 |
(1)下列说法正确的是(选对一个给2分,选对两个给4分,选对三个给6分,选错一个扣3分,最低得分为0分)
| A.布朗运动虽然不是液体分子的运动,但是它可以说明分子在永不停息地做无规则运动 |
| B.只要知道水的摩尔质量和一个水分子的质量,就可以计算出阿伏加德罗常数 |
| C.在使两个分子间的距离由很远(r >10–9 m)减小到很难再靠近的过程中,分子间作用力先减小后增大,分子势能不断增大 |
| D.通过科技创新,我们能够研制出内能全部转化为机械能的热机 |
E.内能不同的物体,它们分子热运动的平均动能可能相同
(2)在粗测油酸分子大小的实验中,具体操作如下:
①取纯油酸1.00mL注入容量为250mL的瓶内,然后向瓶中加入酒精,直到液面达到250mL的刻度为止,摇动瓶使油酸在酒精中充分溶解,形成油酸的酒精溶液;
②用滴管吸取制得的溶液逐滴滴入量筒,记录滴入的滴数直到量筒达到1.00mL为止,恰好共滴了100滴;
③在浅盘内注入约2cm深的水,将痱子粉均匀撒在水面上,再用滴管吸取油酸的酒精溶液,轻轻地向水面滴一滴溶液,油酸在水面上会很快散开,形成一油酸薄膜,待薄膜形状稳定后,将事先准备好的玻璃板放在浅盘上,并在玻璃板上描出油酸薄膜的形状;
④将画有油酸薄膜轮廓形状的玻璃板,放在画有许多已知边长的小正方形的坐标纸上,计算出轮廓范围内正方形的总数,由小正方形边长和小正方形的总个数计算得此油膜面积为3.60×102cm2。
利用上述实验数据可求得油酸分子的直径为 m。(保留3位有效数字)
(3)(9分)如图所示,竖直放置的、左端封闭、右端开口的U形管中用水银柱封住一段空气柱L,当空气柱的温度为t1=7℃时,左臂水银柱的高度h1 =15cm,右臂水银柱的高度h2 =" 10" cm,气柱长度L1=20cm;仅将管内被封住的空气柱加热到t2=127℃且稳定时,图中的h1变为h1′= 10cm。不考虑水银和管的热胀冷缩,大气压强始终不变。当时的大气压强多大?(单位用cmHg)
某热水袋容积为900ml,请估算装水量为80%时热水袋中水分子的数目(阿伏加德罗常数NA=6×1023mol-1)。
利用油膜法可以粗略测出阿伏加德罗常数。把密度ρ=0.8×103kg/m3的某种油,用滴管滴一滴在水面上形成油膜,已知这滴油的体积为V=0.5×10-3cm3,形成的油膜面积为S=0.7m2,油的摩尔质量M=9×10-2kg/mol,若把油膜看成单分子层,每个油分子看成球形,那么:
(1)油分子的直径是多少?
(2)由以上数据可粗略测出阿伏加德罗常数NA是多少?(保留一位有效数字)
已知水的密度ρ=1.0×103 kg/m3、摩尔质量M=1.8×10-2 kg/mol,阿伏加德罗常数NA=6.0×1023 mol-1。试求体积V=360mL的水中含有水分子的总数N和水分子的直径d (结果保留一位有效数字) 。
取一滴油酸酒精溶液滴到水面上,酒精溶于水,油酸在水面上形成一单分子薄膜,测出这一薄膜的面积为0.2m2,已知油酸分子的直径为5×10 -10m,1 cm3的油酸酒精溶液有50滴,试估算原油酸酒精溶液的体积浓度( ×100%).
×100%).