高中物理探究向心力大小与半径、角速度、质量的关系试题

【原创】对做匀速圆周运动的物体，下列关于其向心加速度的说法中正确的是（  ）

A．根据知，向心加速度由速度和轨道半径决定

B．向心加速度的大小保持不变，但向心加速度时刻在变

C．向心加速度的方向时刻指向圆心，所以方向保持不变

D．向心加速度描述速度的方向变化的快慢

如图所示为空间站中模拟地球上重力的装置．环形实验装置的外侧壁相当于“地板” ．让环形实验装置绕O点旋转，能使“地板”上可视为质点的物体与在地球表面处有同样的“重力”，则旋转角速度应为（地球表面重力加速度为g，装置的外半径为R） （ ）

A．

B．

C．2

D．

如图所示，水平转台上放着A、B、C三个物体，质量分别为2m、m、m，离转轴的距离分别为R、R、2R，与转台间的摩擦因数相同，转台旋转时，下列说法中正确的是   （     ）

A.若三个物体均未滑动，C物体的向心加速度最大
B.若三个物体均未滑动，B物体受的摩擦力最大
C.转速增加，A物比B物先滑动
D.转速增加，C物先滑动

“水流星”是一种常见的杂技项目，该运动可以简化为轻绳一端系着小球在竖直平面内的圆周运动模型.已知绳长为l，重力加速度为g，则

A．小球运动到最低点Q时，处于失重状态

B．小球初速度v0越大，则在P、Q两点绳对小球的拉力差越大

C．当时，小球一定能通过最高点P

D．当时，细绳始终处于绷紧状态

(6分)如图所示，在以角速度ω=2rad/s匀速转动的水平圆盘上，放一质量m=5kg的滑块，滑块离转轴的距离r=0.2m，滑块跟随圆盘一起做匀速圆周运动（二者未发生相对滑动）．求：

（1）滑块运动的线速度大小；
（2）滑块受到静摩擦力的大小和方向．
（3）滑块跟随圆盘运动一周过程中静摩擦力所做的功．

如图所示，质量为m的小球在竖直平面内的光滑圆管中做圆周运动，圆的半径为R，小球略小于圆管内径。若小球经过圆管最高点时与轨道间的弹力大小恰为mg，则此时小球的速度为（ ）

A．0

B．

C．

D．

如图所示，为一皮带传动装置，右轮的半径为r，a是它的边缘上的一点，左侧是一轮轴，大轮的半径为4r，小轮的半径为2r，b点在小轮上，到小轮中心距离为r，c点和d点分别位于小轮和大轮的边缘上，若在传动过程中，皮带不打滑，则  （   ）

A．a点与b点线速度大小相等

B．a点与c点角速度大小相等

C．a点与d点向心加速度大小不相等

D．a、b、c、d四点，加速度最小的是b点

质量为m的飞机，以速率v在水平面上做半径为r的匀速圆周运动，空气对飞机的作用力的大小等于                （  ）

A．

B．

C．

D．

如图所示，长为L的轻杆，一端固定一个质量为m的小球，另一端固定在水平转轴O上，杆随转轴O在竖直平面内匀速转动，角速度为ω，某时刻杆对球的作用力恰好与杆垂直，则此时杆与水平面的夹角θ是 （    ）

A．sinθ=

B．tanθ=

C．sinθ=

D．tanθ=

一质点沿半径为R的圆周运动一周，回到原地．它发生的位移大小是（ ）

A．2πR

B．πR

C．2R

D．0

【原创】光滑的圆管轨道半径为L，竖直放置，如图所示，一质量为m的小球在管内运动，已知小球经过最低点的速度为v时，恰好能过最高点，则下列说法正确的是（ ）

A．小球在最高点对圆管内壁的压力为零

B．小球在最高点对圆管内壁的压力为mg

C．小球在最低点时对圆管外壁的压力为

D．小球在最低点时对圆管外壁的压力为

关于向心力的说法中，正确的是（   ）

A．物体由于做圆周运动而产生了一个向心力

B．向心力不改变圆周运动物体的速度

C．做匀速圆周运动的物体其向心力即为其所受的合外力

D．做匀速圆周运动的物体其向心力是不变的

用一根细绳，一端系住一个质量为m的小球，另一端悬在光滑水平桌面上方h处，绳长l大于h，使小球在桌面上做如图所示的匀速圆周运动．若使小球不离开桌面，则小球运动的半径是__________，其转速最大值是__________ 。（已知重力加速度为g）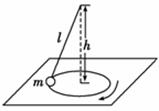

如图所示，甲、乙两水平圆盘紧靠在一块，甲圆盘为主动轮，乙靠摩擦随甲无打滑转动。甲圆盘与乙圆盘的半径之比为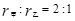，两圆盘和小物体、之间的动摩擦因数相同，距O点为2r，距点为r，当甲缓慢转动起来且转速慢慢增加时（   ）

A．与圆盘相对滑动前与的角速度之比

B．与圆盘相对滑动前与的向心加速度之比

C．随转速慢慢增加，先开始滑动

D．随转速慢慢增加，先开始滑动

如图所示，是马戏团中上演的飞车节目，在竖直平面内有半径为R的圆轨道．表演者骑着摩托车在圆轨道内做圆周运动．已知人和摩托车的总质量为m，人以v₁＝的速度过轨道最高点B，并以v₂＝v₁的速度过最低点A.求在A、B两点轨道对摩托车的压力大小相差多少？