“太极球”是近年来在广大市民中较流行的一种健身器材。做该项运动时,健身者半马步站立,手持太极球拍,拍上放一橡胶太极球,健身者舞动球拍时,球却不会掉落地上。现将太极球简化成如图1所示的平板和小球,熟练的健身者让球在竖直面内始终不脱离板而做匀速圆周运动,且在运动到图1中的A、B、C、D位置时球与板间无相对运动趋势。A为圆周的最高点,C为最低点,B、D与圆心O等高。设球的重力为1N,不计拍的重力。下列说法正确的是
A.健身者在C处所需施加的力比在A处大3N
B.健身者在C处所需施加的力比在A处大1N
C.设在A处时健身者需施加的力为 ,当球运动到B、D位置时,板与水平方向需有一定的夹角
,当球运动到B、D位置时,板与水平方向需有一定的夹角 ,作出的
,作出的 的关系图象为图2
的关系图象为图2
D.设在A处时健身者需施加的力为 ,当球运动到B、D位置时,板与水平方向需有一定的夹角
,当球运动到B、D位置时,板与水平方向需有一定的夹角 ,作出的
,作出的 的关系图象为图3
的关系图象为图3
如图,水平地面上方有绝缘弹性竖直档板,板高h=9m,与板等高处有一水平放置的篮筐,筐口的中心离挡板s=3m.板的左侧以及板上端与筐口的连线上方存在匀强磁场和匀强电场,磁场方向垂直纸面向里,磁感应强度B=1T;质量 、电量
、电量 、视为质点的带电小球从挡板最下端,以某一速度水平射入场中做匀速圆周运动,若与档板相碰就以原速率弹回,且碰撞时间不计,碰撞时电量不变,小球最后都能从筐口的中心处落入筐中(不考虑与地面碰撞后反弹入筐情况),
、视为质点的带电小球从挡板最下端,以某一速度水平射入场中做匀速圆周运动,若与档板相碰就以原速率弹回,且碰撞时间不计,碰撞时电量不变,小球最后都能从筐口的中心处落入筐中(不考虑与地面碰撞后反弹入筐情况), ,求:
,求:
(1)电场强度的大小与方向;
(2)小球从出发到落入筐中的运动时间的可能取值(计算结果可以用分数和保留π值表示)
如图所示,一金属棒AC在匀强磁场中绕平行于磁感应强度方向的轴(过O点)匀速转动,OA=2OC=2L,磁感应强度大小为B、方向垂直纸面向里,金属棒转动的角速度为ω、电阻为r,内、外两金属圆环分别与C、A、D良好接触并从A、D各引出一接线柱与外电阻R相接(没画出),两金属环圆心皆为O且电阻均不计,则( )

A.金属棒中有从A到D的感应电流
B.外电阻R中的电流为
C.当r=2R时,外电阻消耗功率最大
D.金属棒AO间电压为
如图所示,两个通电的彼此绝缘的圆环A、B通有图示的电流,已知两环都可以绕直径COD(C、D为两环交点)自由转动,从左向右看,关于两环转动情况判断正确的是( )

A.A环逆时针转动,B环顺时针转动
B.A环顺时针转动,B环逆时针转动
C.A环逆时针转动,B环逆时针转动
D.A环顺时针转动,B环顺时针转动
如图所示,M是水平放置的半径足够大的圆盘,绕过其圆心的竖直轴 匀速转动,以经过O水平向右的方向作为x轴的正方向 在圆心O正上方距盘面高为h处有一个正在间断滴水的容器,在t=0时刻开始随传送带沿与x轴平行的方向做匀速直线运动,速度大小为v 已知容器在t=0时滴下第一滴水,以后每当前一滴水刚好落到盘面上时再滴一滴水 问:
匀速转动,以经过O水平向右的方向作为x轴的正方向 在圆心O正上方距盘面高为h处有一个正在间断滴水的容器,在t=0时刻开始随传送带沿与x轴平行的方向做匀速直线运动,速度大小为v 已知容器在t=0时滴下第一滴水,以后每当前一滴水刚好落到盘面上时再滴一滴水 问: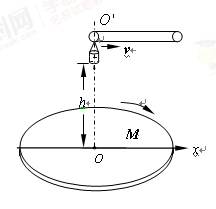
(1)每一滴水经多长时间滴落到盘面上?
(2)要使每一滴水在盘面上的落点都位于一条直线上,圆盘转动的最小角速度ω
(3)第二滴水与第三滴水在盘面上的落点间的最大距离s
一个有一定厚度的圆盘,可以绕通过中心垂直于盘面的水平轴转动,圆盘加速转动时,角速度的增加量△ω与对应时间△t的比值定义为角加速度β。我们用电磁打点计时器、米尺、游标卡尺、纸带、复写纸来完成下述实验:(打点计时器所接交流电的频率为50Hz,A、B、C、D…为计数点,相邻两计数点间有四个点未画出)

①如图甲所示,将打点计时器固定在桌面上,将纸带的一端穿过打点计时器的限位孔,然后固定在圆盘的侧面,当圆盘转动时,纸带可以卷在圆盘侧面上;
②接通电源,打点计时器开始打点,启动控制装置使圆盘匀加速转动;
③经过一段时间,圆盘停止转动和打点,取下纸带,进行测量。
(1)用20分度的游标卡尺测得圆盘的直径如图乙所示,圆盘的直径d为______cm;
(2)由图丙可知,打下计数点D时,圆盘转动的角速度为______rad/s (计算结果保留3位有效数字)
(3)圆盘转动的角加速度大小为______rad/s2。(计算结果保留3位有效数字)
如图所示的竖直向下的匀强电场中,用绝缘的细线拴住的带电小球在竖直平面内绕悬点O做圆周运动,下列说法正确的是 ①带电小球有可能做匀速圆周运动 ②带电小球有可能做变速率圆周运动 ③带电小球通过最高点时,细线拉力一定最小④带电小球通过最低点时,细线拉力有可能最小( )

| A.② | B.①② | C.①②③ | D.①②④ |
如图所示,光滑半球的半径为R,球心为O,固定在水平面上,其上方有一个光滑曲面轨道AB,高度为 .轨道底端水平并与半球顶端相切,质量为m的小球由A点静止滑下,最后落在水平面上的C点.重力加速度为g,则( )
.轨道底端水平并与半球顶端相切,质量为m的小球由A点静止滑下,最后落在水平面上的C点.重力加速度为g,则( )

| A.小球将沿半球表面做一段圆周运动后抛至C点 |
| B.小球将从B点开始做平抛运动到达C点 |
| C.OC之间的距离为2R |
D.小球运动到C点时的速率为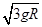 |
如图,长为L的轻杆一端固定质量为m的小球,另一端有固定转轴O.现使小球在竖直平面内做圆周运动.P为圆周轨道的最高点.若小球通过圆周轨道最低点时的速度大小为 ,则以下判断正确的是( )
,则以下判断正确的是( )

| A.小球不能到达P点 |
B.小球到达P点时的速度小于 |
| C.小球能到达P点,但在P点不会受到轻杆的弹力 |
| D.小球能到达P点,且在P点受到轻杆向下的弹力 |
如图所示,在竖直平面内固定的圆形绝缘轨道的圆心为O、半径为r、内壁光滑,A.B两点分别是圆轨道的最低点和最高点,该区域存在方向水平向右的匀强电场,一质量为m、带负电的小球在轨道内侧做完整的圆周运动,(电荷量不变)经过C点时速度最大,O、C连线与竖直方向的夹角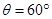 ,CD为直径,重力加速度为g,求
,CD为直径,重力加速度为g,求
(1)小球所受到的电场力的大小
(2)小球在A点速度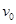 多大时,小球经过D点时对圆轨道的压力最小
多大时,小球经过D点时对圆轨道的压力最小
如图所示,竖直光滑管形圆轨道半径为R(管径远小于R)固定,小球A.b大小相同,质量相同,均为m,其直径略小于管径,能在管中无摩擦运动,两球先后以相同的速度v通过轨道最低点,且当小球a在最低点时,小球b在最高点,以下说法正确的是
A.速度v至少为 时,才能使两球在关内偶完整圆周运动
时,才能使两球在关内偶完整圆周运动
B.速度v至少为 时,才能使两球在关内做完整圆周运动
时,才能使两球在关内做完整圆周运动
C.当小球b在最高点对轨道无压力时,小球a比小球b所需向心力大5mg
D.只要 ,小球a对轨道最低点压力比小球b对轨道最高点压力都大6mg
,小球a对轨道最低点压力比小球b对轨道最高点压力都大6mg
如图所示,一小球从斜轨道的某高度处由静止滑下,然后沿竖直光滑圆轨道的内侧运动,已知圆轨道的半径为R,忽略一切摩擦阻力,则下列说法正确的是
| A.在轨道最低点,最高点,轨道对小球作用力的方向是相同的 |
| B.小球的初位置比圆轨道最低点高出2R时,小球能通过圆轨道的最高点 |
| C.小球的初位置比圆轨道最低点高出0.5R时,小球在运动过程中不脱离轨道 |
| D.小球的初位置只有比圆轨道最低点高出2.5R时,小球在运动过程中才能不脱离轨道 |
如图所示,一质点沿半径R=20m的圆周自A点出发,顺时针方向运动了10s第一次到达B点.求:
(1)这一过程中质点的路程;
(2)这一过程中质点位移的大小和方向;
(3)这一过程中质点平均速度的大小.