长为 的细线一端固定,另一端系一质量为
的细线一端固定,另一端系一质量为 的小球,使小球在竖直平面内做圆周运动(不计空气阻力),小球到最高点时恰好能使线不至松驰,当球位于圆周的最低点时其速率为( )
的小球,使小球在竖直平面内做圆周运动(不计空气阻力),小球到最高点时恰好能使线不至松驰,当球位于圆周的最低点时其速率为( )
A. |
B. |
C. |
D. |
向心加速度的物理意义是( )
| A.描述线速度方向变化的快慢 |
| B.描述线速度大小变化的快慢 |
| C.描述向心力变化的快慢 |
| D.描述角速度变化的快慢 |
关于向心力的下列说法正确的是( )
| A.物体由于做圆周运动而产生了一个向心力 |
| B.向心力只能改变做圆周运动的物体的速度方向,不能够改变速度的大小 |
| C.做匀速圆周运动的物体其向心力指向圆心,所以是恒力 |
| D.做匀速圆周运动的物体其向心力可以改变线速度的大小 |
如图所示,在固定的圆锥形漏斗的光滑内壁上,有两个质量相等的小物块A和B,它们分别紧贴漏斗的内壁,在不同的水平面上做匀速圆周运动。则以下叙述正确的是( )
| A.物块A的线速度小于物块B的线速度 |
| B.物块A的角速度等于物块B的角速度 |
| C.物块A对漏斗内壁的压力等于物块B对漏斗内壁的压力 |
| D.物块A的向心力大于物块B的向心力 |
如图所示,洗衣机脱水桶在转动时,衣服贴靠在匀速转动的圆筒内壁上而不掉下来,则衣服( )
| A.受到4个力的作用 |
| B.所需的向心力由静摩擦力提供 |
| C.所需的向心力由弹力提供 |
| D.所需的向心力由重力提供 |
如图所示,一物体以初速度v0冲向光滑斜面AB,并能沿斜面恰好上升到高度为h的B点,下列说法中正确的是( )
| A.若把斜面从C点锯断,由机械能守恒定律可知,物体冲出C点后仍能升高h |
| B.若把斜面弯成圆弧形AB′,物体仍能沿AB′升高h |
| C.无论是把斜面从C点锯断还是把斜面弯成圆弧形,物体都不能升高h,因为机械能不守恒 |
| D.无论是把斜面从C点锯断还是把斜面弯成圆弧形,物体都不能升高h,但机械能守恒 |
如图,足够大的光滑绝缘水平面上有三个带电质点,A和C围绕B做匀速圆周运动,B恰能保持静止,其中A、C两点与B的距离分别是L1,和L2.不计三质点间的万有引力,则A和C的比荷(电量与质量之比)之比应是
A. B.
B. C.
C. D.
D.
如图所示,在竖直向下的匀强电场中有一绝缘的光滑轨道,一个带负电的小球从斜轨上的A点由静止释放,沿轨道滑下,已知小球的质量为m,电荷量为-q,匀强电场的场强大小为E,斜轨道的倾角为α,圆轨道半径为R,小球的重力大于受的电场力.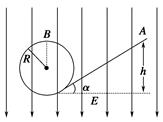
(1)求小球沿轨道滑下的加速度的大小;
(2)若使小球通过圆轨道顶端的B点,求A点距水平地面的高度h至少为多大;
半径为R的绝缘光滑圆环固定在竖直平面内,环上套有一质量为m、带正电的珠子,空间存在水平向右的匀强电场,如图所示.珠子所受静电力是其重力的3/4倍,将珠子从环上最低位置A点由静止释放,求: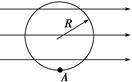
(1)珠子所能获得的最大动能是多少?
(2)珠子对圆环的最大压力是多少?
如图所示,空间存在着场强为E=2.5×102 N/C、方向竖直向上的匀强电场,在电场内一长为L=0.5 m的绝缘细线,一端固定在O点,另一端拴着质量为m=0.5 kg、电荷量为q=4×10-2 C的小球.现将细线拉直到水平位置,使小球由静止释放,当小球运动到最高点时细线受到的拉力恰好达到它能承受的最大值而断裂.取g=10 m/s2.求: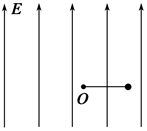
(1)小球的电性;
(2)细线能承受的最大拉力;
(3)当细线断裂后,小球继续运动到与O点水平方向距离为L时(仍在匀强电场中),小球距O点的高度.
如图所示,光滑斜面AB与光滑竖直圆弧轨道BCD在B点平滑连接,质量为m的小物块从斜面上A点由静止释放并滑下,经圆弧轨道最低点C后能沿轨道通过最高点D,此时对D点的压力恰好等于其重力。重力加速度为g,不计空气阻力。求:
(1)物块运动到最低点C时对轨道的压力大小;
(2)A、C的高度差h与圆弧轨道半径R的比值。
由于地球的自转,使得赤道上的物体绕地轴做匀速圆周运动。关于该物体,下列说法中正确的是
| A.向心力等于地球对它的万有引力 |
| B.速度等于第一宇宙速度 |
| C.加速度等于重力加速度 |
| D.周期等于地球同步卫星运行的周期 |
如图所示,某卫星绕地球做匀速圆周运动,则该卫星所受的向心力
| A.大小变化,方向不变 | B.大小不变,方向变化 |
| C.大小和方向都变化 | D.大小和方向都不变 |
如图所示,一辆轿车正在水平路面上转弯,下列说法正确的是
| A.水平路面对轿车弹力的方向斜向上 |
| B.轿车受到的静摩擦力提供转弯的向心力 |
| C.轿车受到的向心力是重力、支持力和牵引力的合力 |
| D.轿车所受的合力方向一定与运动路线的切线方向垂直 |