如图所示,长为L的轻绳一端固定于O点,另一端系一质量为m的小球,现将绳水平拉直,让小球从静止开始运动,重力加速度为g,当绳与竖直方向的夹角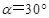 时,小球受到的合力大小为
时,小球受到的合力大小为
A.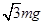 |
B.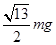 |
C.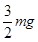 |
D.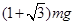 |
如图所示,一根质量不计的轻杆绕水平固定转轴O顺时针匀速转动,另一端固定有一个质量m的小球,当小球运动到图中位置时,轻杆对小球作用力的方向可能
| A.沿F2的方向 | B.沿F1的方向 |
| C.沿F3的方向 | D.沿F4的方向 |
某同学设想驾驶一辆“陆地-太空”两用汽车,沿地球赤道行驶并且汽车相对于地球速度可以增加到足够大。当汽车速度增加到某一值时,它将成为脱离地面绕地球做圆周运动的“航天汽车”。不计空气阻力,已知地球的半径R=6400km。下列说法正确的是
| A.汽车在地面上速度增加时,它对地面的压力增大 |
| B.当汽车速度增加到7.9km/s时,将离开地面绕地球做圆周运动 |
| C.此“航天汽车”环绕地球做圆周运动的最小周期为1h |
| D.在此“航天汽车”上可以用弹簧测力计测量物体的重力 |
如图所示,x轴与水平传送带重合,坐标原点O在传送带的左端,传送带长L=8 m,匀速运动的速度v0=5 m/s。一质量m=1 kg的小物块轻轻放在传送带上xP=2 m的P点,小物块随传送带运动到Q点后恰好能冲上光滑圆弧轨道的最高点N点。小物块与传送带间的动摩擦因数μ=0.5,重力加速度g=10 m/s2。求:
(1)N点的纵坐标;
(2)小物块在传送带上运动产生的热量;
(3)若将小物块轻放在传送带上的某些位置,小物块均能沿光滑圆弧轨道运动(小物块始终在圆弧轨道运动不脱轨)到达纵坐标yM=0.25 m的M点,求这些位置的横坐标范围。
如图所示为空间站中模拟地球上重力的装置.环形实验装置的外侧壁相当于“地板” .让环形实验装置绕O点旋转,能使“地板”上可视为质点的物体与在地球表面处有同样的“重力”,则旋转角速度应为(地球表面重力加速度为g,装置的外半径为R) ( )
A. |
B.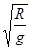 |
C.2 |
D.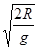 |
如图所示光滑管形圆轨道半径为R(管径远小 于R),小球a、b大小相同,质量均为m,其直径略小于管径,能在管中无摩擦运动.两球先后以相同速度v通过轨道最低点,且当小球a在最低点时,小球b在最高点,以下说法正确的是( )
| A.当小球b在最高点对轨道无压力时,小球a比小球b所需向心力大5mg |
B.当 时,小球b在轨道最高点对轨道无压力 时,小球b在轨道最高点对轨道无压力 |
C.速度v至少为 ,才能使两球在管内做圆周运动 ,才能使两球在管内做圆周运动 |
D.只要 ,小球a对轨道最低点的压力比小球b对轨道最高点的压力大6mg ,小球a对轨道最低点的压力比小球b对轨道最高点的压力大6mg |
如图所示,质量为m=0.2kg的小球固定在长为L=0.9m的轻杆的一端,杆可绕O点的水平转轴在竖直平面内转动。(g=10 m/s2)求:
(1)当小球在最高点的速度为多大时,球对杆的作用力为零?
(2)当小球在最高点的速度分别为6 m/s 和1.5 m/s 时,球对杆的作用力的大小与方向?
【改编】如图所示,位于竖直平面上半径为R=0.2m的1/4圆弧轨道AB光滑无摩擦,O点为圆心。质量为m=1kg的小球从A点由静止释放,到达B点时,小球对轨道的压力为30N,从B点飞出,最后落在地面C处。若BC所连直线与水平方向夹角为θ,且tanθ=1,取g ="10" m/s2,不计空气阻力,求:
(1)小球通过B点时的速度 ;
;
(2)B点与水平地面的高度差H;
(3)小球落地时的速度大小。
乘坐游乐园的翻滚过山车时,质量为m的人随车一起在竖直平面内旋转,下列说法正确的是( )
| A.车的加速度方向时刻在变化,但总是指向圆心 |
| B.人在最高点时对座位仍可能产生压力,但是速度可以为零 |
| C.车的线速度方向时刻在变化,但总在圆周切线方向上 |
| D.人在最底点时对座位的压力大于mg |
如图所示,一可视为光滑的玻璃小球,设其可在碗内不同的水平面上做匀速圆周运动,下列说法正确的是 ( )

| A.玻璃球越靠近碗口其对碗的压力越大 |
| B.玻璃球越靠近碗口其向心加速度越小 |
| C.玻璃球越靠近碗口其线速度一定越大 |
| D.玻璃球的重力与碗内壁对它的弹力的合力提供球做圆周运动所需的向心力 |
如图所示,质量为m的小球在竖直平面内的光滑圆管中做圆周运动,圆的半径为R,小球略小于圆管内径。若小球经过圆管最高点时与轨道间的弹力大小恰为mg,则此时小球的速度为( )

| A.0 | B. |
C. |
D. |
【改编】有关圆周运动的基本模型,下列说法正确的是( )
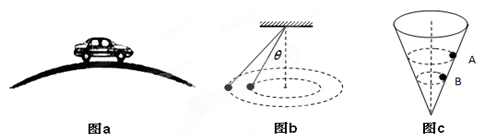
A.如图a,汽车通过拱桥的最高点时的速度越大,汽车对拱桥的压力就越大
B.如图b所示是一圆锥摆,减小θ,但保持圆锥的高不变,则θ越小,圆锥摆的周期越小
C.如图c,同一小球在光滑而固定的圆锥筒内的A、B位置先后分别做匀速度圆周运动,则在A、B两位置小球的角速度及所受筒壁的支持力大小相等
D.火车转弯时的速度小于规定速度行驶时,内轨对内轮缘会有挤压作用
如图,置于圆形水平转台边缘的小物块随转台加速转动,当转速达到某一数值时,物块恰好滑离转台开始做平抛运动.现测得转台半径R=0.5 m,离水平地面的高度H=0.8 m,物块平抛落地过程水平位移的大小s=0.4 m.设物块所受的最大静摩擦力等于滑动摩擦力,取重力加速度g=10 m/s2.求: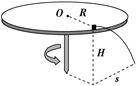
(1)物块做平抛运动的初速度大小v0;
(2)物块与转台间的动摩擦因数μ.
(9分) 如图所示,水平轨道AB与竖直半圆形光滑轨道在B点平滑连接,半圆形轨道半径R=2.5m,质量m=0.1kg的小滑块(可视为质点)以一定的速度从水平轨道进入半圆形轨道,沿轨道运动恰好能到最高点C,且从C点水平飞出后恰好落在A点,重力加速度g=10m/s2,试分析求解:
(1)滑块通过C点时的速度大小;
(2)AB间的距离x。
铁路转弯处的弯道半径r是由地形决定的,弯道处要求外轨比内轨高,其内、外轨高度差h的设计不仅与r有关,还与火车在弯道上的行驶速率v有关。下列说法正确的是( )
| A.速率v一定时,r越大,要求h越大 |
| B.速率v一定时,r越小,要求h越大 |
| C.半径r一定时,v越小,要求h越大 |
| D.半径r一定时,v越大,要求h越大 |