一辆汽车以54km/h的速率通过一座拱桥的桥顶,汽车对桥面的压力等于车重的一半,这座拱桥的半径是 m。若要使汽车过桥顶时对桥面无压力,则汽车过桥顶时的速度大小至少是 m/s。
用一根细绳,一端系住一个质量为m的小球,另一端悬在光滑水平桌面上方h处,绳长l大于h,使小球在桌面上做如图所示的匀速圆周运动.若使小球不离开桌面,则小球运动的半径是__________,其转速最大值是__________ 。(已知重力加速度为g)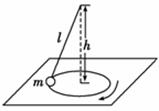
一圆环,其圆心为O,若以它的直径AB为轴做匀速转动,如图所示.

(1)圆环上P、Q两点的线速度大小之比是 ;
(2)若圆环的半径是R,绕AB轴转动的周期是T,则环上Q点的向心加速度大小是 ;
(3)P点的向心加速度的方向是 .
一辆质量为4t的汽车驶过半径为50m的凸形桥面时,始终保持5m/s的速率,汽车所受阻力为车与桥面间压力的0.05倍,求通过最高点时汽车对桥面的压力为 ,此时汽车的牵引力大小为
质量为1000kg的汽车,行驶到一座半径为40m的圆形凸桥顶时,如果汽车队桥的压力恰好为零,则此时汽车所需向心力大小为N,汽车的速度大小为m/s(g取10m/s )
)
质量为1000kg的汽车,行驶到一座半径为40m的圆形凸桥顶时,如果汽车队桥的压力恰好为零,则此时汽车所需向心力大小为 N,汽车的速度大小为 m/s(g取10m/s )
)
如图所示,长0.40m的细绳,一端拴一质量为0.2kg的小球,在光滑水平面上绕绳的
另一端做匀速圆周运动,若运动的角速度为5.0rad/s,绳对小球需施多大拉力___________
如图,在探究向心力公式的实验中,为了探究物体质量、圆周运动的半径、角速度与向心力的关系,运用的试验方法是 法 ;现将小球分别放在两边的槽内,为探究小球受到的向心力大小与角速度大小的关系,做法正确的是:在小球运动半径 (填“相等”或“不相等”)的情况下,用质量 (填“相同”或“不相同”)的钢球做实验。
长为L="0.5" m的轻杆,其一端固定于O点,另一端连着质量m=1kg的小球,小球绕O点在竖直平面内做圆周运动,当它通过最高点速度v="3" m/s时,小球受到细杆的作用力为大小为 N,是 。(填“拉力”或“支持力”)(g=10m/s2)
如图所示,细线下面悬挂一个小钢球(可看作质点),让小钢球在水平面内做匀速圆周运动。若测得小钢球作圆周运动的圆半径为r,悬点O到圆心O’之间的距离为h,小球质量为m。忽略空气阻力,重力加速度为g。小球做匀速圆周运动的周期T= 。
一个圆盘在水平面内匀速转动,盘面上有一个小物体随圆盘一起运动,此时小物体所受摩擦力的方向为_________。若已知小物体与圆盘间的最大静摩擦因数为μ,且小物体所在位置到圆盘圆心的距离为L,则要保持小物体与圆盘相对静止的条件是:圆盘转动的角速度不得超过_________。
长度1m的细绳,一端固定于光滑水平桌面上,另一端拴接一个质量为2kg的小球,若小球以4m/s的速度在桌面上做匀速圆周运动,则小球的向心加速度大小为a向=__________m/s2,所需向心力大小为__________N.