高中物理探究单摆的周期与摆长的关系填空题

一个单摆摆长为l，摆球质量为m，最大摆角为α，重力加速度为g。规定平衡位置为零势能处，则摆球摆动的周期等于___   ________，摆动过程中摆球的最大重力势能等于_____   ______，摆球的最大速度等于__ _____  ____。

已知地球和月球的质量分别为M和m，半径分别为R和r。在地球上和月球上周期相等的单摆摆长之比为________，摆长相等的单摆在地球上和月球上周期之比为________。

用单摆可以测定重力加速度。摆长为的单摆在偏角很小时的摆动，可以看成是简谐运动，其固有周期T=__________，由此可得g=__________。只要测出摆长l和周期T，即可计算出当地的重力加速度值。如图所示，让刻度尺的零点对准摆线的悬点，摆线竖直下垂。若摆球直径为2.00cm，则单摆的摆长=__________cm。

利用单摆测量某地的重力加速度，现测得摆球质量为m，摆长为L，通过传感器测出摆球运动时位移随时间变化的规律为，则该单摆的振动周期为      ，该处的重力加速度g=        ；若减小振幅A，则周期      （选填“增大”、“减小”或“不变”）．

利用单摆测量某地的重力加速度，现测得摆球质量为m，摆长为L，通过传感器测出摆球运动时位移随时间变化的规律为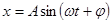，则该单摆的振动周期为       ，该处的重力加速度g=         ；若减小振幅A，则周期       （选填“增大”、“减小”或“不变”）．

一个单摆的振动周期是2s，求下列作简谐运动情况下单摆的周期：
（1）摆长缩短为原来的1/4，单摆的周期为________s；
（2）摆球的质量减为原来的1/4，单摆的周期为________s；
（3）振幅减为原来的1/4，单摆的周期为________s。

如图所示的实线和虚线分别表示同一个单摆在A、B两个星球半径大小相同的星球表面上的振动图象，其中实线是A星球上的，虚线是B星球上的，那么两个星球的平均密度ρ_A和ρ_B之比是__________。

如图所示,为同一个单摆分别在地球和月球上做受迫振动的共振曲线,则图线__________表示的是在地球上单摆的共振曲线,可以求得该单摆的摆长为__________m,月球表面的重力加速度约为__________ m/s².

某人利用单摆来确定某高山的高度。已知单摆在海面处的周期是T₀。而在该高山上，测得该单摆周期为T。则此高山离海平面高度h为             。（把地球看作质量均匀分布的半径为R的球体）

如左图所示是利用沙摆演示简谐运动图象的装置。当盛沙的漏斗下面的薄木板被水平匀速拉出时，做简谐运动的漏斗漏出的沙在板上形成的曲线显示出沙摆的振动位移随时间的变化关系，已知木板被水平拉动的速度为，右图所示的一段木板的长度为，重力加速度为，漏沙时不计沙摆的重心变化。则这次实验沙摆的振动周期    ，摆长      。

如图，小球质量为m，摆长为L，最大摆角为θ，且小于5º.小球在竖直平面内摆动。则在图示位置时摆线的拉力为             。从最高点第一次摆到最低点的时间为                     。（重力加速度为g）

（1）利用单摆测重力加速度的实验中，偏角小于5⁰，但测出的重力加速度的数值偏大，可能原因是_________

A．振幅较小	B．测摆长时，只量出摆线的长度，没有从悬挂点量到摆球中心
C．数振动次数时，少计了一次	D．数振动次数时，多计了一次

(2)利用单摆测重力加速度的实验中，为了减小测量周期的误差，应在______位置（填“最低点”或“最高点”）开始计时和结束计时.

（1）实验室中有一种游标卡尺，其游标尺有10格，总长为19mm。游标上每格比主尺上2 mm少0.1mm，故其精度为0.1mm。如图所示，用这种游标卡尺测量小球的直径，则直径为_________mm。

（2）某同学欲测一单摆的周期，如果测得单摆完成30次全振动时秒表的示数如图所示，那么秒表的读数是________s，该单摆的摆动周期是_________s。（保留三位有效数字）