细长轻绳下端拴一小球构成单摆，在悬挂点正下方
摆长处有一个能挡住摆线的钉子A，如图所示．现将单摆向左方拉开一个小角度然后无初速度释放．对于单摆的运动，下列说法中正确的是( )．
| A．摆球往返运动一次的周期比无钉子时的单摆周期小 |
| B．摆球在左、右两侧上升的最大高度一样 |
| C．摆球在平衡位置左右两侧走过的最大弧长相等 |
| D．摆球在平衡位置右侧的最大摆角是左侧的2倍 |
如图甲所示是用沙摆演示振动图像的实验装置，此装置可视为摆长为L的单摆，沙摆的运动可看作简谐运动，实验时在木板上留下图甲所示的结果。若用手拉木板做匀速运动，速度大小是v。图乙所示的一段木板的长度是s。下列说法正确的是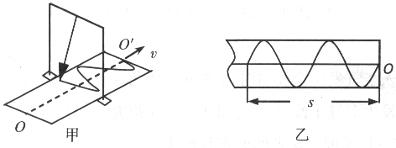
| A．可估算出这次实验所用沙摆对应的摆长 |
| B．若增大手拉木板的速度，则沙摆的周期将变大 |
| C．若减小沙摆摆动时的最大摆角，则沙摆的周期将变小 |
| D．若增大沙摆的摆长，保持拉动木板的速度不变，则仍将得到与图乙完全相同的图样 |
如图甲所示是演示沙摆振动图像的实验装置在木板上留下的实验结果。沙摆的运动可看作是简谐运动。若手用力F向外拉木板作匀速运动，速度大小是0.20m/s．图14乙是某次实验得到的木板的长度为0.60m范围内的振动图像，那么这次实验所用的沙摆的摆长为________cm。（答案保留2位有效数字，计算时可以取
）
一个单摆和一个弹簧振子，在上海调节使得它们的振动周期相等(设为T)．现在把它们一起拿到北京，若不再做任何调节．设这时单摆的振动周期为T1，弹簧振子的振动周期为T2，则它们的周期大小的关系为( )．
| A．T1<T2＝T | B．T1＝T2<T | C．T1>T2＝T | D．T1<T2<T |
单摆做简谐运动的回复力是（ ）
| A．摆球的重力 |
| B．摆球所受重力与悬线对摆球的拉力的合力 |
| C．悬线对摆球的拉力 |
| D．摆球所受重力在圆弧切线方向上的分力 |
如图所示，曲面AO是一段半径为2m的光滑圆弧面，圆弧与水平面相切于O点，AO弧长10cm．现将一小球先后从曲面的顶端A和AO弧的中点B由静止释放，到达底端O的速度分别为v1和v2，所经历的时间分别是t1和t2，那么（ ）
| A．v1＞v2，t1＞t2 |
| B．v1=v2， t1＞t2 |
| C．v1＞v2，t1=t2 |
| D．v1=v2， t1=t2 |
如图所示，A、B分别为单摆做简谐振动时摆球的不同位置.其中，位置A为摆球摆动的最高位置，虚线为过悬点的竖直线.以摆球最低位置为重力势能零点，则摆球在摆动过程中
A、位于B处时动能最大
B、位于A处时势能最大
C、在位置A的势能大于在位置B的动能
D、在位置B的机械能大于在位置A的机械能
一个摆长为l1的单摆，在地面上做简谐运动，周期为T1，已知地球的质量为M1，半径为R1，另一摆长为l2的单摆，在质量为M2，半径为R2的星球表面做简谐运动，周期为T2.若T1＝2T2，l1＝4l2，M1＝4M2，则地球半径与星球半径之比R1∶R2为( )．
| A．2∶1 | B．2∶3 | C．1∶2 | D．3∶2 |
如图所示，用绝缘细线悬吊着的带正电小球在匀匀强磁场中做简谐运动，则( )
| A．当小球每次通过平衡位置时，动能相同 |
| B．当小球每次通过平衡位置时，速度相同 |
| C．当小球每次通过平衡位置时，丝线拉力相同 |
| D．撤消磁场后，小球摆动周期变化 |
已知在单摆a完成10次全振动的时间内，单摆b完成了6次全振动，两摆长之差为1.6 m．则两单摆长La与Lb分别为( )．
| A．La＝2.5 m，Lb＝0.9 m | B．La＝0.9 m，Lb＝2.5 m |
| C．La＝2.4 m，Lb＝4.0 m | D．La＝4.0 m，Lb＝2.4 m |
如图所示，单摆甲放在空气中，周期为T甲，单摆乙带正电，放在匀强磁场中，周期为T乙，单摆丙带正电，放在匀强电场中，周期T丙，单摆丁放在静止在水平面上的光滑斜面上，周期为T丁，那么( )
| A．T甲>T乙>T丙=>T丁 |
| B．T乙>T甲=T丙>T丁 |
| C．T丙>T甲>T丁=>T乙 |
| D．T丁>T甲=T乙>T丙 |
做简谐振动的单摆摆长不变，若摆球质量增加为原来的4倍，摆球经过平衡位置时速度减小为原来的1/2，则单摆振动的( )
| A．频率、振幅都不变 | B．频率、振幅都改变 |
| C．频率不变，振幅改变 | D．频率改变，振幅不变 |
如图所示，一单摆悬于O点，摆长为L，若在O点的竖直线上的O′点钉一个钉子，使OO′＝L/2，将单摆拉至A处释放，小球将在A、B、C间来回振动，若振动中摆线与竖直方向夹角小于10°，则此摆的周期是( )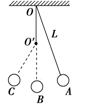
A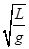．2π
B．2π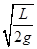
C．2π(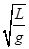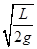＋ ) D．π(＋ )
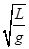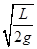粤公网安备 44130202000953号