将一单摆向左拉至水平标志线上，从静止释放，当摆球运动到最低点时，摆线碰到障碍物，摆球继续向右摆动。用频闪照相机拍到如图所示的单摆运动过程的频闪照片，以下说法正确的是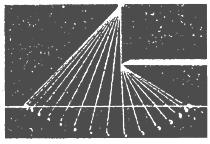
| A．摆线碰到障碍物前后的周期之比为3:2． |
| B．摆线碰到障碍物前后的摆长之比为3：2 |
| C．摆球经过最低点时，线速度变小，半径减小，摆线张力变大 |
| D．摆球经过最低点时，角速度变大，半径减小，摆线张力不变 |
房顶上固定着一根不可伸长的细线，下垂到三楼窗沿下，某同学应用单摆原理测量窗的上沿到房顶的高度，先将线的下端系上一个小球，发现当小球静止时，细线恰好与窗子上沿接触且保持竖直，他打开窗子，让小球在垂直于墙的竖直平面内摆动，如图所示，从小球第1次通过图中的B点开始计时，第21次通过B点用时30s；球在最低点B时，球心到窗上沿的距离为1m，当地重力加速度取g=π2（m/s2）；根据以上数据可得小球运动的周期T=_______s；房顶到窗上沿的高度h=_______m。
如图甲所示是演示沙摆振动图像的实验装置在木板上留下的实验结果。沙摆的运动可看作是简谐运动。若手用力F向外拉木板作匀速运动，速度大小是0.20m/s．图14乙是某次实验得到的木板的长度为0.60m范围内的振动图像，那么这次实验所用的沙摆的摆长为________cm。（答案保留2位有效数字，计算时可以取
）
如图所示，圆心在O点、半径为R的圆弧轨道abc竖直固定在水平桌面上,Oc与Oa的夹角为60°，轨道最低点a与桌面相切. 一轻绳两端系着质量为m1和m2的小球（均可视为质点），挂在圆弧轨道边缘c的两边，开始时，m1位于c点，然后从静止释放，设轻绳足够长，不计一切摩擦。则
| A．在m1由c下滑到a的过程中，两球速度大小始终相等 |
| B．m1在由c下滑到a的过程中重力的功率先减少后增大 |
| C．若m1恰好能沿圆弧下滑到a点，则m1=2m2 |
| D．若m1恰好能沿圆弧下滑到a点，则m1=3m2 |
如图所示，两根细线长度均为2m，A细线竖直悬挂且在悬点O处穿有一个金属小球a，B悬挂在悬点
处，细线下端系有一金属小球b，并且有ma>mb，把金属小球b向某一侧拉开3cm到
处，然后同时让金属小球a、b由静止开始释放（不计阻力和摩擦），则两小球的最终情况是
| A．a小球先到达最低点，不可能和b小球在最低点相碰撞； |
| B．b小球先到达最低点，不可能和a小球在最低点相碰撞； |
| C．a、b两小球恰好在最低点处发生碰撞； |
| D．因不知道ma、mb的具体数值，所以无法判断最终两小球的最终情况。 |
如图所示，光滑的圆弧槽的半径为R（R＞＞弧MN），A为弧形槽的最低点，小球B放在A点正上方离A点的高度为h，小球C放在M点，同时释放两球，使两球正好在A点相碰，则h应多大？
利用单摆测量某地的重力加速度，现测得摆球质量为m，摆长为L，通过传感器测出摆球运动时位移随时间变化的规律为
。则该单摆的振动周期T= ，该处的重力加速度g= ；若减小振幅A，则周期 （选填“增大”、“减小”或“不变”）。
如图所示为同一实验室中两个单摆的振动图像。从图象可以知道它们的 （ ）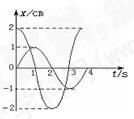
| A．摆长相等 |
| B．振幅相等 |
| C．摆球同时改变速度方向 |
| D．摆球质量差1 倍 |
如图所示，放置在水平地面上的支架质量为M，支架顶端用细线拴着的摆球质量为m，现将摆球拉至水平位置，而后释放，摆球运动过程中，支架始终不动，以下说法正确的是（ ）
| A．在释放前的瞬间，支架对地面的压力为（m+M）g |
| B．在释放前的瞬间，支架对地面的压力为mg |
| C．摆球到达最低点时，支架对地面的压力为（m+M）g |
| D．摆球到达最低点时，支架对地面的压力为（3m+M）g |
如图所示，单摆摆球的质量为m，摆长为L，摆球从最大位移A处由静止释放，摆球运动到最低点B时的速度大小为v。重力加速度为g，不计空气阻力。则摆球从A运动到B的过程中
A．重力做的功为 |
| B．重力的最大瞬时功率为mgv |
| C．重力的功率先增大后减小 |
D．摆球运动到最低点B时绳的拉力为  |
如图所示，一台玩具电机的轴上安有一个小皮带轮甲，通过皮带带动皮带轮乙转动（皮带不打滑），皮带轮乙上离轴心O距离2mm处安有一个圆环P．一根细绳一端固定在圆环P上，另一端固定在对面的支架上，绳呈水平方向且绷直．在绳上悬挂着4个单摆a．b．c．d．已知电动机的转速是150r/min，甲、乙两皮带轮的半径之比为1︰5，4个单摆的摆长分别是100cm、80cm、60cm、40cm．电动机匀速转动过程中，哪个单摆的振幅最大（ ）
| A．单摆a | B．单摆b | C．单摆c | D．单摆d |
已知单摆a完成10次全振动的时间内，单摆b完成6次全振动，两摆长之差为1.6m，则两摆长la和lb分别为 （ ）
| A．la=2.5m， lb=0.9m | B．la=0.9m， lb=2.5m |
| C．la=2.4m， lb=4.0m | D．la=4.0m， lb=2.4m |
一个摆长为l1的单摆，在地面上做简谐运动，周期为T1，已知地球质量为M1，半径为R1，另一摆长为l2的单摆，在质量为M2，半径为R2的星球表面做简谐运动，周期为T2，若T1＝2T2，l1＝4l2，M1＝4M2，则地球半径与星球半径之比R1∶R2为（ ）
| A．2∶1 | B．2∶3 | C．1∶2 | D．3∶2 |
如图所示是一个单摆振动的情形，O是它的平衡位置，B、C是摆球所能到达的最远位置．设摆球向右方向运动为正方向．图1-3-16所示是这个单摆的振动图像．根据图像回答：(取π2＝10)
甲 乙
(1)单摆振动的频率是多大？
(2)开始时刻摆球在何位置？
(3)若当地的重力加速度为10 m/s2，试求这个摆的摆长是多少？
粤公网安备 44130202000953号