高中物理探究单摆的周期与摆长的关系试题

同一地点有甲、乙两个单摆，当甲摆动了120次时，乙恰好摆动了80次，则甲、乙两摆的摆长之比是

A．2∶3

B．3∶2

C．4∶9

D．9∶4

如图所示，用两根长度都为l的细线悬挂一个小球A，两悬挂点等高，线与水平天花板间的夹角都是α，使球A在垂直于纸面的平面内做小幅度的摆动，当A经过平衡位置的瞬间，另一小球B从A球的正上方自由下落，若B球恰能击中A球，求B球开始下落时离A球振动平衡位置的高度。

有两个单摆做简谐运动，位移与时间关系是：x₁=3asin(4πbt+)和x₂=9asin(8πbt+)，其中a、b为正的常数，则它们的：振幅之比为__________；摆长之比为_________。

一个单摆在甲地时，在时间t内完成m次全振动，移至乙地时，经过相同的时间完成n次全振动，则甲、乙两地重力加速度大小之比g_甲：g_乙等于______________。

某同学在用单摆测定重力加速度的实验中，测量不同摆长情况下单摆的振动周期，并以L为横坐标，为纵坐标，做出了图线，如图所示，由此图线可知重力加速度为            m/s²。　　　　　　　　　　　　　　　　　　　

如右图甲所示，有一质量为m、带电量为+q的小球在竖直平面内做单摆，摆长为L，当地的重力加速度为g，则周期T=        ；若在悬点处放一带正电的小球（图乙），则周期将        。（填“变大”、“不变”、“变小”）

两个摆长相同的单摆，摆球质量之比是4:1，在不同地域振动，当甲摆振动4次的同时，乙摆恰振动5次，则甲、乙二摆所在地区重力加速度之比为             。

下图甲是一个单摆振动的情形，O是它的平衡位置，B、C是摆球所能到达的最远位置，设摆球向右方向运动为正方向，下图乙是这个单摆的振动图象，根据图象回答：

(1)单摆振动的频率是多大？
(2)开始时刻摆球在何位置？
(3)若当地的重力加速度为9.86 m/s²， 试求这个摆的摆长是多少？

如右图甲所示，有一质量为m、带电量为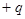的小球在竖直平面内做单摆，摆长为L，当地的重力加速度为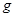，则周期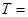        ；若在悬点处放一带正电的小球（图乙），则周期将        。（填“变大”、“不变”、“变小”）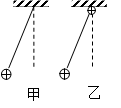

如图所示，半径是0.2m的圆弧状光滑轨道置于竖直面内并固定在地面上，轨道的最低点为B，在轨道的A点（弧AB所对圆心角小于5°）和弧形轨道的圆心O两处各有一个静止的小球Ⅰ和Ⅱ，若将它们同时无初速释放，先到达B点的是________球

如图所示，是一个单摆（θ<10^o），其周期为T，则下列正确的说法是（  ）

A．把摆球的质量增加一倍，其周期变小

B．把摆角变小时，则周期也变小

C．此摆由O→B运动的时间为T/4

D．摆球B→O时，动能向势能转化

下列说法中正确的是

A．把调准的摆钟，由北京移至赤道，这个钟将变慢，若要重新调准，应增加摆长

B．振动的频率越高，则波传播一个波长的距离所用的时间越短

C．1905年爱因斯坦提出的狭义相对论是以相对性原理和光速不变原理这两条基本假设为前提的

D．调谐是电磁波发射应该经历的过程，调制是电磁波接收应该经历的过程

有人利用安女装在气球载人舱内的单摆来确定气球的高度．已知该单摆在海平面处的周期是T₀，当气球停在某一高度时，测得该单摆周期为了，求该气球此时离海平面的高度h．把地球看作质量均匀分布的半径为只的球体．

一个单摆，如果摆球的质量增加为原来的4倍，摆球经过平衡位置时的速度减为原来的，则单摆的

A．频率不变，振幅不变	B．频率不变，振幅改变
C．频率改变，振幅不变	D．频率改变，振幅改变

下列说法中正确的是         。

A．弹簧振子的周期与振幅无关，单摆运动到平衡位置时合外力为0

B．同一地点的单摆摆长越长，其振动周期越长

C．纵波可以沿水平方向传播，也可以沿竖直方向传播

D．在波传播方向上的某个质点的振动速度就是波的传播速度