高中物理力学实验实验题

利用单摆测重力加速度的实验中，如果偏角足够小，但测出的重力加速度的数值偏大，可能原因是                                        （   ）

A．振幅较小

B．测摆长时，只量出摆线的长度，没有从悬挂点量到摆球中心

C．数振动次数时，少计了一次

D．数振动次数时，多计了一次

某同学设计了如图（）所示电路研究电源输出功率变化情况。电源电动势、内电阻恒定，为滑动变阻器，、为定值电阻，、为理想电表。

（1）若滑动片由滑至时示数一直变小，则和必须满足的关系是。
（2）若＝6，＝12，电源内电阻＝6，，当滑动片由滑至时，电源E的输出功率随外电路总电阻的变化关系如图（）所示，则的阻值应该选择（）

A．

2

B．

4

C．

6

D．

8

某兴趣小组想要探究单摆的周期T与摆长、摆球质量m的关系：
（1）为了探究周期T与摆长、摆球质量m的关系，应利用_________法完成此实验；为了准确测量单摆的周期，应使摆球振动稳定后且经过_________位置开始计时。
（2）他们在探究周期T与摆长的关系时，测得如下5组数据，请在图中选择恰当坐标，作出直观反映周期T与摆长关系的图像。

数值   　　　　次数 项目	1	2	3	4	5
	1.78	1.90	1.99	2.10	2.19
（）	3.19	3.60	3.99	4.40	4.79
（）	0.80	0.90	1.00	1.10	1.20
（）	0.64	0.81	1.00	1.21	1.44

（3）根据图像求得当地的重力加速度g=___________m/s²。（保留三位有效数字）
（4）某学生做实验时固定好装置后先测摆长，然后测出周期，发现测得的重力加速度偏大，原因可能是______（填选项前字母）

A．单摆的悬点未固定紧，振动中出现松动，使摆线增长了

B．把摆球n次经过最低点的时间误记为(n + 1)次经过最低点的时间

C．计时结束时，秒表过早按下

D．单摆所用摆球质量过大

（1）某同学在做“利用单摆测重力加速度”实验中，先测得摆线长为97.50cm；摆球直径为2.00 cm；然后用秒表记录了单摆振动50次所用的时间为99.9s．则
①该摆摆长为_______cm，周期为       s
②如果他测得的g值偏小，可能的原因是 [   ]

A．测摆线长时摆线拉得过紧
B．摆线上端未牢固地系于悬点，振动中出现松动，使摆线长度增加了
C．开始计时，秒表过迟按下	D．实验中误将49次全振动数为50次

（2）在一次用单摆测定加速度的实验中，图A的O点是摆线的悬挂点，a、b点分别是球的上沿和球心，摆长L=      m. 秒表读数__________
为了提高测量精度,需多次改变L的值并测得相应的T值.现测得的六组数据标示在以L为横坐标、T²为纵坐标的坐标纸上,即图中用“”表示的点。根据图中的数据点作出T²与L的关系图线.

用单摆测重力加速度时
（1）摆球应采用直径较小,密度尽可能_____的球,摆线长度要在1米以上,用细而不易______的尼龙线；
（2）摆线偏离竖直方向的角度θ应_______；
（3）要在摆球通过________位置时开始计时,摆线每经过此位置______次才完成一次全振动；
（4）摆球应在________面内摆动,每次计时时间内,摆球完成全振动次数一般选为___      ____次。利用单摆测重力加速度的实验中，摆长的测量应在摆球自然下垂的状况下从悬点量至                。某同学组装了如图所示的单摆，并用图示的L作为摆长，这样测得的g值将偏     。（填“大”或“小”）

“验证力的平行四边形定则”实验中

（1）部分实验步骤如下，请完成有关内容：
A．将一根橡皮筋的一端固定在贴有白纸的竖直平整木板上，另一端绑上两根细线．
B．在其中一根细线挂上5个质量相等的钩码，使橡皮筋拉伸，如图(1)所示，记录：      、      、        ．
C．将步骤B中的钩码取下，分别在两根细线上挂上4个和3个质量相等的钩码，用两
光滑硬棒B、C使两细线互成角度，如图(2)所示，小心调整B、C的位置，使   ，记录   ．
（2）如果“力的平行四边形定则”得到验证，那么图(2)中=       ．

有人说矿区的重力加速度偏大，某兴趣小组用单摆测定重力加速度的实验探究该问题。（1）用刻度尺测得摆长为，测量周期时用到了秒表，长针转一周的时间为30s，表盘上部的小圆共15大格，每一大格为1min，该单摆摆动n=50次时，长短针的位置如图所示，所用时间为t=________s。



（2）用以上直接测量的物理量的英文符号表示重力加速度的计算式为g=__________（不必代入具体数据）。
（3）若有一位同学在实验时测出多组单摆的摆长l和运动周期T，作出T²—图象，就可以求出矿区的重力加速度.理论上T²—图象是一条过坐标原点的直线，该同学根据实验数据作出的图象如图所示.
①造成图象不过坐标原点的原因最有可能是___________。
②由图象求出的重力加速度g＝_______m/s²（取π²=9.87）。

某同学利用如图甲的实验装置探究测量重力加速度大小。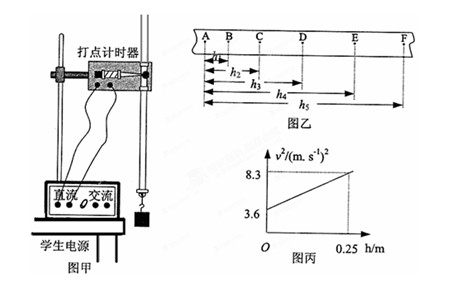

（1）该同学开始实验时情形如图甲所示，接通电源释放纸带。请指出该同学在实验操作中存在的两处明显错误或不当的地方：
①                                                ；
②                                                                  。
（2）该同学经修改错误并正确操作后得到如图乙所示的纸带，取连续六个点A、B、C、D、E、F为计数点，测得A点到B、C、D、E、F的距离分别为h₁、h₂、h₃、h₄、h₅。若打点的频率为f，则打E点时重物的速度表达式V_E=              ；该同学先分别计算出各计数点的速度值，并试画出速度的二次方(V²)与对应重物下落的距离（h）的关系如图丙所示，则重力加速度g=               m/s²。

有一秒摆T="2" s，摆球的质量为0.04 kg，当摆球质量增加到0.08 kg时，它的周期是_______，当摆长增加到原来的4倍时，它的振动频率是_________。

一个秒摆摆球的质量为0.2 kg，它振动到最大位移时距最低点的高度为0.4 cm，它完成10次全振动回到最大位移时，距最低点的高度变为0.3 cm，如果每完成10次全振动给它补充一次能量，使摆球回到原来的高度，在60 s内总共补充的能量是____________________.

在“用单摆测定重力加速度”的实验中，用刻度尺测量悬点到小球的距离为96.60 cm，用卡尺量得小球直径是5.260 cm，测量周期有3次，每次是在摆球通过最低点时，按下秒表开始计时，同时将此次通过最低点作为第一次，接着一直数到计时终止，结果如下表.

	1	2	3
数的次数	61	81	71
时间（s）	60.40	79.80	70.60

这个单摆振动周期的测定值是_______________s，当地重力加速度的值是__________m/s².（取三位有效数字）

某同学在“利用单摆测重力加速度”的实验中，先测得摆线长为97.50 cm，摆球直径为2.00 cm，然后用秒表记录了单摆振动50次所用的时间，如图11-4所示，则

图11-4
（1）该摆摆长为 ____________cm，秒表所示读数为____________s.
（2）如果他测得的g值偏小，可能的原因是____________.

A．测摆线长时测了悬线的总长度

B．摆线上端未牢固地系于悬点，振动中出现松动，使摆线长度增加了，使周期变大了

C．开始计时时，秒表过迟按下

D．实验中误将49次全振动数次数记为50次

（3）为了提高实验精度，在实验中可改变几次摆长l并测出相应的周期T，从而得出一组对应的l与T的数据如图11-5，再以l为横坐标，T²为纵坐标将所得数据连成直线，并求得该直线的斜率为k，则重力加速度g=________________.（用k表示）

图11-5

将在地球上校准的摆钟拿到月球上去，若此钟在月球记录的时间是1 h，那么实际的时间应是______________h(月球表面的重力加速度是地球表面的1/6).若要把此摆钟调准，应使摆长L₀调节为______________.

如图11-4-11所示是演示沙摆振动图象的实验装置，沙摆的运动可看作简谐运动.若用手向外拉木板的速度是0.20 m/s，木板的长度是0.60 m，那么这次实验所用的沙摆的摆长为__________ m.（答案保留两位有效数字，计算时可取π²=g）

图11-4-11

两个单摆甲和乙，它们的摆长之比为4∶1，若它们在同一地点做简谐运动，则它们的周期之比T_甲∶T_乙=__________；在甲摆完成10次全振动的时间内，乙摆完成的全振动次数为__________.