高中物理力学实验实验题

某物理兴趣小组的同学在研究弹簧弹力的时候，测得弹力的大小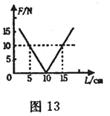
F和弹簧长度L的关系如图13所示，则由图线可知：
（1）弹簧的劲度系数为                  。
（2）弹簧的弹力为5N，弹簧的长度为        。

用弹簧测力计称量一物体时，测力计指针所指位置如图所示，这个力是 　_N．该弹簧测力计的最小刻度值是   _，用这个弹簧秤称量的力的大小不能超过　　 N．

图甲是一个单摆振动的情形，O是它的平衡位置，B、C是摆球所能到达的最远位置．设摆球向右方向运动为正方向．图乙是这个单摆的振动图象．根据图象回答：

(1)单摆振动的频率是      
(2)开始时刻摆球的位置是         
(3)若当地的重力加速度为10 m/s²，摆长是       

“单摆的周期T与摆长L的关系”的实验中，某次测量小球的直径的示数如图1所示，图中游标上10格的长度为19mm，则小球的直径d为         mm。用秒表记下了单摆振动50次的时间如图2所示，由图可读出时间为          s。

（2）有两位同学利用假期分别去参观北京大学和南京大学的物理实验室，各自在那里利用先进的DIS系统较准确地探究了“单摆的周期T与摆长L的关系”，他们通过校园网交换实验数据，并由计算机绘制了T²－L图象，如图甲所示．去北大的同学所测实验结果对应的图线是        (填“A”或“B”)．另外，在南大做探究的同学还利用计算机绘制了两种单摆的振动图象如图乙所示，由图可知，两单摆的摆长之比＝         ．

如图实－11－5所示是用来验证动量守恒的实验装置，弹性球1用细线悬挂于O点，O点正下方桌子的边沿有一竖直立柱．实验时，调节悬点，使弹性球1静止时恰与立柱上的球2接触且两球等高．将球1拉到A点，并使之静止，同时把球2放在立柱上．释放球1，当它摆到悬点正下方时与球2发生对心碰撞．碰后球1向左最远可摆到B点，球2落到水平地面上的C点．测出有关数据即可验证1、2两球碰撞时动量守恒．现已测出A点离水平桌面的距离为a.B点离水平桌面的距离为b，C点与桌子边沿间的水平距离为c.此外：
(1)还需要测量的量是______________、________________和________________．
(2)根据测量的数据，该实验中动量守恒的表达式为________________________．(忽略小球的大小)

某同学在做“利用单摆测重力加速度”的实验中，先测得摆线长为101.00cm，摆球直径为2.00cm，然后用秒表记录了单摆振动50次所用的时间为101.5 s。则：
（1）他测得的重力加速度g =          m/s².（计算结果取三位有效数字）
(2) 他测得的g值偏小，可能原因是：          

A．测摆线长时摆线拉得过紧。

B．摆线上端未牢固地系于悬点，振动中出现松动，使摆线长度增加了。

C．开始计时时，秒表过迟按下。

D．实验中误将49次全振动计为50次。

（3）为了提高实验精度，在实验中可改变几次摆长l并测出相应的周期T，从而得出一组对应的l和T的数值，再以l为横坐标、T²为纵坐标将所得数据连成直线，并求得该直线的斜率K。则重力加速度g =          。（用K表示）

某同学利用如图所示的装置测量当地的重力加速度。实验步骤如下：

A．按装置图安装好实验装置；
B．用游标卡尺测量小球的直径d；
C．用米尺测量悬线的长度；
D．让小球在竖直平面内小角度摆动。当小球经过最低点时开始计时，
并计数为0，此后小球每经过最低点一次，依次计数1、2、3……。
当数到20时，停止计时，测得时间为t；
E．多次改变悬线长度，对应每个悬线长度，都重复实验步骤C、D；
F．计算出每个悬线长度对应的t ²；
G．以t ²为纵坐标、为横坐标，作出t ²－图线。
结合上述实验，完成下列任务：
（1）用游标为10分度的游标卡尺测量小球的直径。某次测量的示数如下图所示，读出小球直径d的值为          cm。

（2）该同学根据实验数据，利用计算机作出t ²–图线如图所示。根据图线拟合得到方程
t ²＝404.0 ＋3.0。由此可以得出当地的重力加速度g＝          m/s²。
（取π ² ＝ 9.86，结果保留3位有效数字）

（3）从理论上分析图线没有过坐标原点的原因，下列分析正确的是 （     ）
A．不应在小球经过最低点时开始计时，应该在小球运动到最高点开始计时；
B．开始计时后，不应记录小球经过最低点的次数，而应记录小球做全振动的次数；
C．不应作t ² –图线，而应作t –图线；
D．不应作t ² –图线，而应作t ² –（+d）图线。

某同学在做“利用单摆测重力加速度”实验中，先测得摆线长为97.20cm；用20分度的游标卡尺测小球直径如图4所示，然后用秒表记录了单摆全振动50次所用的时间为100.0s．则

（1）记录时间应从摆球经过_______________开始计时，小球直径为___________cm， 测得重力加速度g值为             m/s²（保留小数点后两位有效数字）
（2）如果他在实验中误将49次全振动数为50次，测得的g值         (填“偏大”或“偏小”或“准确”）
（3）如果该同学在测摆长时忘记了加摆球的半径，则测量结果         (填“偏大”或“偏小”或“准确”）；但是他以摆长（l）为纵坐标、周期的二次方（T²）为横坐标作出了l－T²图线，由图象测得的图线的斜率为k，则测得的重力加速度g=         。（用字母表示即可）。此时他用图线法求得的重力加速度       。（选填“偏大”，“偏小”或“准确”）

在测定某电阻的伏安特性曲线中，待测金属丝的电阻R_x约为5 Ω，实验室备有下列实验器材
A．电压表(量程0～3 V，内阻约为15 kΩ)
B．电压表(量程0～15 V，内阻约为75 kΩ)
C．电流表(量程0～3 A，内阻约为0.2 Ω)
D．电流表(量程0～0.6 A，内阻约为11 Ω)
E．变阻器R₁(0～10 Ω，0.6 A)
F．变阻器R₂(0～2000 Ω，0.1 A )
G．电池组E(电动势为3 V，内阻约为0.3 Ω)
H．开关S，导线若干
(1)为减小实验误差，应选用的实验器材有(填代号)　　　　．
(2) 为了尽可能减少误差，请你在虚线框中画出本实验的电路图.
(3)测量结果比真实值偏　　　　。﹙大、小、无法确定﹚
(4)若此电阻为金属丝绕制而成，用螺旋测微器测得该金属丝的直径如图所示，则金属丝的直径为________mm.

质量为2㎏的物体，静止于水平面上，从t = 0时刻开始对物体施加水平力F₁和竖直向下的力F₂的作用。已知F₁=" 6" t (N)、F₂ = 4 t (N)，水平面对物体的最大静摩擦力等于压力的0.5倍，那么，t =1s时，物体受到的摩擦力大小为_______N；t =______s时，物体开始运动。（取g =10m/s²）

画出图中小球和杆所受的力的示意图（接触面光滑），请在答卷纸上直接画出示意图

在《用单摆测定重力加速度》的实验中：
（1）某同学用秒表测得单摆完成40次全振动的时间如图(a)所示，则单摆的周期为       s。

（2）实验中对提高测量结果精度有利的建议是______。

A．单摆的摆线不能太短

B．单摆的摆球密度尽可能大

C．单摆的摆角越大越好

D．从平衡位置开始计时，测量一次全振动的时间作为摆动周期

（3）若单摆在任意摆角θ时的周期公式可近似为T=T₀[1+asin²(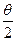)]，式中T₀为摆角趋近于0°时的周期，a为常数；为了用图象法验证该关系式，需要测量的物理量有________；某同学在实验中得到了如图(b)所示的图线，则图线的斜率表示_______。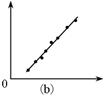

利用单摆测重力加速度的实验中，如果偏角足够小，但测出的重力加速度的数值偏大，可能原因是                                        （   ）

A．振幅较小

B．测摆长时，只量出摆线的长度，没有从悬挂点量到摆球中心

C．数振动次数时，少计了一次

D．数振动次数时，多计了一次

某兴趣小组想要探究单摆的周期T与摆长、摆球质量m的关系：
（1）为了探究周期T与摆长、摆球质量m的关系，应利用_________法完成此实验；为了准确测量单摆的周期，应使摆球振动稳定后且经过_________位置开始计时。
（2）他们在探究周期T与摆长的关系时，测得如下5组数据，请在图中选择恰当坐标，作出直观反映周期T与摆长关系的图像。

数值   　　　　次数 项目	1	2	3	4	5
	1.78	1.90	1.99	2.10	2.19
（）	3.19	3.60	3.99	4.40	4.79
（）	0.80	0.90	1.00	1.10	1.20
（）	0.64	0.81	1.00	1.21	1.44

（3）根据图像求得当地的重力加速度g=___________m/s²。（保留三位有效数字）
（4）某学生做实验时固定好装置后先测摆长，然后测出周期，发现测得的重力加速度偏大，原因可能是______（填选项前字母）

A．单摆的悬点未固定紧，振动中出现松动，使摆线增长了

B．把摆球n次经过最低点的时间误记为(n + 1)次经过最低点的时间

C．计时结束时，秒表过早按下

D．单摆所用摆球质量过大

（1）某同学在做“利用单摆测重力加速度”实验中，先测得摆线长为97.50cm；摆球直径为2.00 cm；然后用秒表记录了单摆振动50次所用的时间为99.9s．则
①该摆摆长为_______cm，周期为       s
②如果他测得的g值偏小，可能的原因是 [   ]

A．测摆线长时摆线拉得过紧
B．摆线上端未牢固地系于悬点，振动中出现松动，使摆线长度增加了
C．开始计时，秒表过迟按下	D．实验中误将49次全振动数为50次

（2）在一次用单摆测定加速度的实验中，图A的O点是摆线的悬挂点，a、b点分别是球的上沿和球心，摆长L=      m. 秒表读数__________
为了提高测量精度,需多次改变L的值并测得相应的T值.现测得的六组数据标示在以L为横坐标、T²为纵坐标的坐标纸上,即图中用“”表示的点。根据图中的数据点作出T²与L的关系图线.