高中物理力学实验计算题

如图所示，一个横截面积S=10cm²的容器中，有一个用弹簧和底部相连的活塞，活塞质量不计，当温度为27℃时，内外压强都为p=1×10⁵Pa，活塞和底面相距L=20cm。在活塞上放质量m=20kg的物体，活塞静止时下降10cm，温度仍为27℃，不计活塞与容器壁的摩擦，g=10m/s²。求：
i.弹簧的劲度系数k；
ii.如果把活塞内气体加热到57℃，为保持活塞静止时位置仍下降10cm，活塞上应冉加物体的质量为多少。

如图所示，ABCD竖直放置的光滑绝缘细管道，其中AB部分是半径为R的圆弧形管道，BCD部分是固定的水平管道，两部分管道恰好相切于B。水平面内的M、N、B三点连线构成边长为L等边三角形，MN连线过C点且垂直于BCD。两个带等量异种电荷的点电荷分别固定在M、N两点，电荷量分别为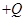和。现把质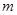量为、电荷量为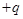的小球（小球直径略小于管道内径，小球可视为点电荷），由管道的A处静止释放，已知静电力常量为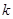，重力加速度为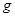。求：

（1）小球运动到B处时受到电场力的大小；
（2）小球运动到C处时的速度大小；
（3）小球运动到圆弧最低点B处时，小球对管道压力的大小。

某同学利用玩具电动车模拟腾跃运动。如图所示，AB是水平地面，长度为L=6m，BCDE是一段曲面，且在B点处平滑连接。玩具电动车的功率始终为P=10W，从A点由静止出发，到达离地面h=1.8m的E点水平飞出，落地点与E点的水平距离x=2.4m。玩具电动车可视为质点，总质量为m=1kg，重力加速度g取10m/s²，不计空气阻力。求：

（1）玩具电动车过E点时的速度；
（2）若玩具电动车在AB段所受的阻力F_f恒为2N，从B点到E点的过程中，克服摩擦阻力做功10J，则从A点至E点过程所需要的时间是多少?

粗糙水平轨道AB与竖直平面内的光滑圆弧轨道BC相切于B点，一物块（可看成为质点）在水平向右的恒力F作用下自水平轨道的P点处由静止开始匀加速运动到B，此时撤去该力，物块滑上圆弧轨道，在圆弧轨道上运动一段时间后，回到水平轨道，恰好返回到P点停止运动，已知物块在圆弧轨道上运动时对轨道的压力最大值为F₁=2.02N，最小值为F₂=1.99N，当地重力加速度为g=10m/s²．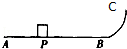

（1）求物块的质量m的大小；
（2）若已知圆弧轨道的半径为R=8m，P点到B点的距离是x=0.5m，求F的大小．

如图，水平轨道AB与竖直固定圆轨道相切于B点，C为圆轨道最高点，圆轨道半径R=5m．一质量m=60kg的志愿者，驾驶质量M=940kg、额定功率P=40kW的汽   车体验通过圆轨道时所受底座的作用力，汽车从A点由静止以加速度a=2m／s²做匀   加速运动，到达B点时，志愿者调节汽车牵引力，使汽车匀速率通过圆轨道又回到B点，志愿者在C点时所受底座的支持力等于志愿者的重力，已知汽车在水平轨道及圆轨道上的阻力均为汽车对轨道压力的0.1倍，取g=10m／s²，计算中将汽车视为质点。
求：

(1)汽车在C点的速率；
(2)汽车在C点的牵引功率；
(3)AB间的距离及汽车从A点经圆轨道又回到B点的过程所用的时间。

如图，在光滑的倾角为θ的固定斜面上放一个劈形的物体A，其上表面水平，质量为M．物体B质量为m，B放在A的上面，先用手固定住A．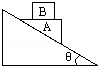

（1）若A的上表面粗糙，放手后，求AB相对静止一起沿斜面下滑，B对A的压力大小．
（2）若A的上表面光滑，求放手后的瞬间，B对A的压力大小．

“太空粒子探测器”是由加速、偏转和收集三部分组成，其原理可简化如下：如图1所示，辐射状的加速电场区域边界为两个同心平行半圆弧面，圆心为O，外圆弧面AB的电势为 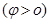，内圆弧面CD的电势为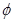，足够长的收集板MN平行边界ACDB，ACDB与MN板的距离为L．假设太空中漂浮着质量为m，电量为q的带正电粒子，它们能均匀地吸附到AB圆弧面上，并被加速电场从静止开始加速，不计粒子间的相互作用和其它星球对粒子的影响，不考虑过边界ACDB的粒子再次返回。

（1）求粒子到达O点时速度的大小；
（2）如图2所示，在PQ（与ACDB重合且足够长）和收集板MN之间区域加一个匀强磁场，方向垂直纸面向内，则发现均匀吸附到AB圆弧面的粒子经O点进入磁场后最多有能打到MN板上，求所加磁感应强度的大小；
（3）如图3所示，在PQ（与ACDB重合且足够长）和收集板MN之间区域加一个垂直MN的匀强电场，电场强度的方向如图所示，大小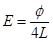，若从AB圆弧面收集到的某粒子经O点进入电场后到达收集板MN离O点最远，求该粒子到达O点的速度的方向和它在PQ与MN间运动的时间。

如图，在水平轨道右侧固定半径为R的竖直圆槽形光滑轨道，水平轨道的PQ段铺设特殊材料，调节其初始长度为l，水平轨道左侧有一轻质弹簧左端固定，弹簧处于自然伸长状态．可视为质点的小物块从轨道右侧A点以初速度v₀冲上轨道，通过圆形轨道、水平轨道后压缩弹簧，并被弹簧以原速率弹回．已知R=0.4m，l=2.5m，v₀=6m/s，物块质量m=1kg，与PQ段间的动摩擦因数μ=0.4，轨道其它部分摩擦不计．取g=10m/s²．求：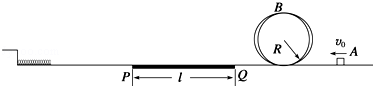

（1）物块经过圆轨道最高点B时对轨道的压力；
（2）物块从Q运动到P的时间及弹簧获得的最大弹性势能；
（3）物块仍以v₀从右侧冲上轨道，调节PQ段的长度l，当l长度是多少时，物块恰能不脱离轨道返回A点继续向右运动．

如图所示，光滑水平面上，轻弹簧两端分别拴住质量均为m的小物块A和B，B物块靠着竖直墙壁。今用水平外力缓慢推A，使A、B间弹簧压缩，当压缩到弹簧的弹性势能为E时撤去此水平外力，让A和B在水平面上运动。求：
①当弹簧达到最大长度时A、B的速度大小；
②当B离开墙壁以后的运动过程中，弹簧弹性势能的最大值。

一转动装置如图甲所示，两根足够长轻杆OA、OB固定在竖直轻质转轴上的O点，两轻杆与转轴间夹角均为30°，小球a、b分别套在两杆上，小环c套在转轴上，球与环质量均为m，c与a、b间均用长为L的细线相连，原长为L的轻质弹簧套在转轴上，且与轴上P点、环c相连。当装置以某一转速转动时，弹簧伸长到，环c静止在O处，此时弹簧弹力等于环的重力，球、环间的细线刚好拉直而无张力。弹簧始终在弹性限度内，忽略一切摩擦和空气阻力，重力加速度为g。求：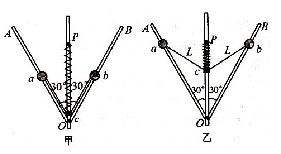

（1）细线刚好拉直而无张力时，装置转动的角速度ω₁
（2）如图乙所示，该装置以角速度ω₂（未知）匀速转动时，弹簧长为L/2，求此时杆对小球的弹力大小；
（3）该装置转动的角速度由ω₁缓慢变化到ω₂，求该过程外界对转动装置做的功。

如图所示，水平绝缘粗糙的轨道AB与处于竖直平面内的半圆形绝缘光滑轨道BC平滑连接，半圆形轨道的半径R=0.40m．在轨道所在空间存在水平向右的匀强电场，电场线与轨道所在的平面平行，电场强度E=1.0×10⁴N/C．现有一电荷量q=+1.0×10^﹣4C，质量m=0.10kg的带电体（可视为质点），在水平轨道上的P点由静止释放，带电体恰好能通过半圆形轨道的最高点C，然后落至水平轨道上的D点．取g=10m/s²．试求：

（1）带电体在圆形轨道C点的速度大小．
（2）D点到B点的距离x_DB．
（3）带电体运动到圆形轨道B点时对圆形轨道的压力大小．
（4）带电体在从P开始运动到落至D点的过程中的最大动能．

如图所示，在光滑绝缘的水平面上，放置两块直径为2L的同心半圆形金属板A、B，两板间的距离很近，半圆形金属板A、B的左边有水平向右的匀强电场E₁，半圆形金属板A、B之间存在电场，两板间的电场强度E₂可认为大小处处相等，方向都指向O，现从正对A、B板间隙、到两板的一端距离为d处静止释放一个质量为m、电荷量为q的带正电微粒（不计重力），此微粒恰能在两板间运动且不与板发生相互作用．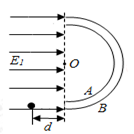

（1）求半圆形金属板A、B之间电场强度的E₂的大小？
（2）从释放微粒开始，经过多长时间微粒的水平位移最大？

一个重30N的物体置于斜面上，如图，斜面的倾斜角为30°，挡板竖直，不计一切摩擦．（取g=10m/s²）

（1）画出小球受力分析示意图．
（2）求出斜面和挡板对小球的作用力．

如图所示，质量M=kg的木块套在水平杆上，并用轻绳将木块与质量m=kg的小球相连悬在空中。今用跟水平方向成α=30°角的力F=N拉着球带动木块一起向右匀速运动，运动中M、m相对位置保持不变，取g=10m/s²。求：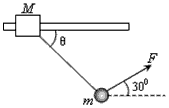

（1）运动过程中轻绳与水平方向夹角θ；
（2）木块与水平杆间的动摩擦因数为μ.

如图所示，固定的光滑平台左端固定有一光滑的半圆轨道，轨道半径为R，平台上静止放着两个滑块A、B，其质量m_A=m，m_B =2m，两滑块间夹有少量炸药．平台右侧有一小车，静止在光滑的水平地面上，小车质量M=3m，车长L=2R，车面与平台的台面等高，车面粗糙，动摩擦因数μ=0.2，右侧地面上有一立桩，立桩与小车右端的距离为S，S在0<S<2R的范围内取值，当小车运动到立桩处立即被牢固粘连。点燃炸药后，滑块A恰好能够通过半圆轨道的最高点D，滑块B冲上小车．两滑块都可以看作质点，炸药的质量忽略不计，爆炸的时间极短，爆炸后两个滑块的速度方向在同一水平直线上，重力加速度为g=10m/s²．求：

（1）滑块A在半圆轨道最低点C受到轨道的支持力F_N。
（2）炸药爆炸后滑块B的速度大小v_B。
（3）请讨论滑块B从滑上小车在小车上运动的过程中，克服摩擦力做的功W_f与S的关系。