如图所示,长度为L=1m的绳,系一小球在竖直平面内做圆周运动,小球的质量为M=0.5kg,小球直径不计,小球通过最低点时的速度大小为v=2m/s,试计算:
(1)小球在最低点的向心加速度;
(2)小球在最低点所受绳子的拉力。(g取10m/s2)
如图所示,在光滑的圆锥顶用长为L的细线悬挂一质量为m的小球,圆锥顶角为2θ,当圆锥和球一起以角速度ω匀速转动时,球压紧锥面。
(1)此时绳的张力是多少?
(2)若要小球离开锥面,则小球的角速度至少为多少?
质量是30kg的小孩坐在秋千板上,小孩离系绳子的横梁的距离为3m.如果秋千摆到最低点时,小孩的速度大小是3m/s,试计算此时秋千板对小孩的支持力是多大?(g取10m/s2)
如图所示为一轻质弹簧的长度l和弹力F大小的关系图象,试由图线确定: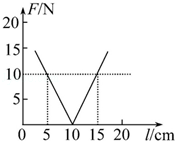
(1)弹簧的原长;
(2)弹簧的劲度系数;
(3)弹簧长为0.20m时弹力的大小.
如图所示,细绳一端系着质量M=0.6 kg的物体,静止于水平面上,另一端通过光滑小孔吊着质量m=0.3 kg的物体,M的中点与圆孔距离为0.2 m,并知M和水平面的最大静摩擦力为2 N.现使此平面绕中心轴线转动,问角速度ω在什么范围m会处于静止状态?(g取10 m/s2)
一人先向北走了40m,耗时10s,随即又向东行走了30m,耗时又是10s。
试求:(1)此人在前10s内的位移和路程
(2)在整个20s内的平均速度的大小和平均速率(sin37°=0.6;cos37°=0.8)
在用高级沥青铺设的高速公路上,汽车的设计时速是108km/h。汽车在这种路面上行驶时,它的轮胎与地面的最大静摩擦力等于车重的0.6倍。如果汽车在这种高速路的水平弯道上拐弯,假设弯道的路面是水平的,其弯道的最小半径是多少?如果高速路上设计了圆弧拱桥做立交桥,要使汽车能够安全通过圆弧拱桥,这个圆弧拱桥的半径至少是多少?
在倾角为30°的斜面上,固定一挡板,在挡板和斜面之间放置同一重为G=20N密度均匀的光滑圆球,如图甲和乙所示两种情况.甲图中的挡板保持竖直,乙图中的档板保持与斜面垂直,圆球处于静止状态,试分别求出两种情况下斜面对球作用力的大小.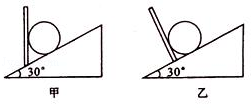
一辆质量为2吨的汽车由静止开始沿一倾角为300的足够长斜坡向上运动,汽车发动机的功率保持48kW不变,行驶120m后达到最大速度。已知汽车受到地面的摩擦阻力为2000N。(g=10m/s2)求:
(1)汽车可以达到的最大速度
(2)汽车达到最大速度所用的时间(结束保留一位小数)
某同学在做“探究弹力和弹簧伸长的关系”的实验时,将一轻弹簧竖直悬挂并让其自然下垂,测出其自然长度;然后在其下部施加外力F,测出弹簧的总长度L,改变外力F的大小,测出几组数据,作出外力F与弹簧总长度L的关系图线如图所示.(实验过程是在弹簧的弹性限度内进行的)由图可知该弹簧的自然长度为 cm;该弹簧的劲度系数为 N/m.

质量为m的汽车沿平直公路行驶,发动机的额定功率为P0.当它的加速度为a时,速度为v,此时发动机的实际功率为P1.假设运动中所受阻力恒定,则它在平直公路匀速行驶的最大速度是多少?(实际功率不超过额定功率)
如图所示,半径为r=1m的长圆柱体绕水平轴OO′以角速度ω=2rad/s匀速转动,将一质量为m=1kg的物体A(可看作质点)放在圆柱体的正上方,并用平行于转轴的光滑挡板(图中未画出),挡住使它不随着圆柱体一起转动而下滑,物块与圆柱体间动摩擦因数为0.4。现用平行于水平转轴的力F推物体,使物体以a=2m/s2的加速度,向右由静止开始匀加速滑动并计时,整个过程没有脱离圆柱体,重力加速度g取10m/s2,则:
(1)若没有推力F,滑块静止于圆柱体上时,挡板对滑块的弹力大小
(2)存在推力F时,F是否为恒力,若是求其大小;若不是,求其大小与时间的关系
(3)存在推力F时,带动圆柱体匀速转动的电动机输出功率与时间关系
小球用一条不可伸长的轻绳相连接,绳的另一端固定在悬点上。当小球在竖直面内来回摆动(如图甲所示),用力传感器测得绳子对悬点的拉力大小随时间变化的曲线(如图乙所示)。已知绳长为1.6m,绳子的最大偏角θ=60 o,g=10m/s2,试求:
(1)小球的质量m;
(2)小球经过最低时的速度v。