以下是对公式的理解及物理学史上的重大发现,其中说法正确的有
A.由公式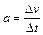 知,物体的加速度等于速度的变化率 知,物体的加速度等于速度的变化率 |
| B.伽利略根据实验证实了力是使物体运动的原因 |
| C.开普勒发现了万有引力定律 |
| D.由公式F=ma知,一定质量的物体所受合外力由运动加速度a决定 |
在公路的每个路段都有交通管理部门设置限速标志如图所示,这是告诫驾驶员在这一路段驾驶车辆时
| A.必须以这一规定速度行驶 |
| B.平均速度大小不得超过这一规定数值 |
| C.瞬时速度大小不得超过这一规定数值 |
| D.汽车上的速度计指示值,有时还是可以超过这一规定值的 |
汽车电动机启动时车灯会瞬时变暗,如图图,在打开车灯的情况下,电动机未启动时电流表读数为,电动机启动时电流表读数为
,若电源电动势为
,内阻为0.05
,电流表内阻不计,则因电动机启动,车灯的电功率降低了()

| A. |
|
B. |
|
C. |
|
D. |
|
如图所示,一轻质细绳的下端系一质量为m的小球,绳的上端固定于O点。现用手将小球拉至水平位置(绳处于水平拉直状态),松手后小球由静止开始运动。在小球摆动过程中绳突然被拉断,绳断时与竖直方向的夹角为α。已知绳能承受的最大拉力为F,若想求出cosα值,你有可能不会求解,但是你可以通过一定的物理分析,对下列结果自的合理性做出判断。根据你的判断cosα值应为 ( )
A. |
B. |
C. |
D. |
如图所示,一轻质弹簧竖直立在水平地面上,弹簧一端固定在地面上。一小球从高处自由下落到弹簧上端,将弹簧压缩至最低点。在小球开始下落至最低点的过程中,弹簧始终处于弹性限度内。在此过程中,能正确表示小球的加速度a随下降位移x的大小变化关系是下面图像中的 ( )

如图所示,单摆摆球的质量为m,做简谐运动的周期T,摆球从最大位移A处由静止开始释放,摆球运动到最低点B时的速度为v,则 ( )
A.摆球从A运动到B的过程中重力的平均功率为 |
B.摆球从A运动到B的过程中重力的冲量为 |
C.摆球运动到B时重力的瞬时功率是 |
D.摆球从A运动到B的过程中合力做的功为 |
在国际单位制(SI)中,下列物理量单位属于基本单位的是( )
A.牛顿(N) B.焦耳(J) C.安培(A) D.库仑(C)
如图所示,一些商场安装了智能化的自动扶梯。为了节约能源,在没有乘客乘行时,自动扶梯以较小的速度匀速运行,当有乘客乘行时自动扶梯经过先加速再匀速两个阶段运行。则电梯在运送乘客的过程中
| A.乘客始终受摩擦力作用 |
| B.乘客经历先超重再失重 |
| C.乘客对扶梯的作用力先指向右下方,再竖直向下 |
| D.扶梯对乘客的作用力始终竖直向上 |
在空气阻力大小恒定的条件下,小球从空中下落,与水平地面相碰后弹到空中某一高度。以向下为正方向,其速度随日寸、问变化的关系如图所示,取g=10m/s2,则以下结论正确的是( )
| A.小球能弹起的最大高度为1m |
| B.小球能弹起的最大高度为0.45 m |
| C.小球弹起到最大高度的时刻如t2=0.80s |
| D.空气阻力与重力的比值为1:5 |
汽车在平直的公路上行驶,某一段时间内汽车的功率随时间的变化如图所示,设汽车运动过程中受到的阻力不变,则在这一段时间内汽车的运动情况可能是 ( )
| A.匀速直线运动 |
| B.匀加速直线运动 |
| C.加速度增加的加速直线运动 |
| D.加速度减小的加速直线运动 |

下面叙述均选自2008年北京奥运会比赛项目的一段,存在克服重力做功的过程是跳水比赛中①、运动员从10米高的跳台上跃入水中;②、运动员从水底迅速浮出水面。举重比赛中③、运动员艰难的挺举起110kg的杠铃;④、运动员举起杠铃后向前走了两步停下。马术比赛中⑤、运动员骑马迅速冲上山坡;⑥运动员骑马在水平跑道上冲过终点后减速。( )
| A.①④⑥ | B.②③⑤ | C.⑥②③ | D.⑤①③ |
在地球大气层外有很多太空垃圾绕地球做匀速圆周运动,每到太阳活动期,由于受太阳的影响,地球大气层的厚度开始增加,从而使得部分垃圾进入大气层,开始做靠近地球的向心运动,产生这一结果的原因是 ( )
| A.由于太空垃圾受到地球引力减小而导致的向心运动 |
| B.由于太空垃圾受到地球引力增大而导致的向心运动 |
| C.由于太空垃圾受到空气阻力而导致的向心运动 |
| D.地球引力提供了太空垃圾做圆周运动所需的向心力,故产生向心运动的结果与空气阻力无关 |
一单摆做小角度摆动,其振动图象如图,以下说法正确的是 
| A.t1时刻摆球速度最大,悬线对它的拉力最小 |
| B.t2时刻摆球速度为零,悬线对它的拉力最小 |
| C.t3时刻摆球速度为零,悬线对它的拉力最大 |
| D.t4时刻摆球速度最大,悬线对它的拉力最大 |
关于物体运动的速度和加速度的关系,下列说法正确的是:( )
| A.速度越大,加速度也越大 |
| B.速度变化越快,加速度一定越大 |
| C.加速度的方向保持不变,速度方向也一定保持不变 |
| D.加速度就是增加的速度 |