汽车刹车后做匀减速直线运动，最后停了下来，在刹车过程中，汽车前半程的平均速度与后半程的平均速度之比是
A． ∶1 |
B．1∶ |
C．1∶（＋1） |
D．（＋1）∶1 |
物体作匀加速直线运动，已知加速度为2m／s２，那么 （）
| A．任意１秒时间内物体的末速度一定等于初速度的2倍 |
| B．任意１秒时间内物体的末速度一定比初速度大2m／s |
| C．第5s的初速度一定比第4s的末速度大2m／s |
| D．第5s的末速度一定比第4s的初速度大2m／s |
—质点沿x轴做直线运动，其v-t图像如图所示。质点在t=0时位于x=3m处，开始沿x轴正方向运动。当t=7s.时，质点在轴上的位置坐标为
| A．x="3.5m" | B．x=6.5m | C．x=9m | D．x=11.5m |
如图所示，直线甲和曲线乙分别是在平直公路上行驶的汽车甲和乙的位移—时间（x-t）图线，由图可知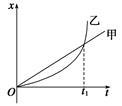
| A．t1时刻乙车追上甲车 |
| B．t1时刻乙车速度大于甲车速度 |
| C．0到t1时间内，乙车速度一直小于甲车的速度 |
| D．0到t1时间内，乙车的平均速度小于甲车的平均速度 |
静止在光滑水平面上的物体受到一个水平拉力的作用，该力随时间变化的关系如图所示，则下列结论正确的是（ ）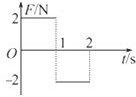
| A．拉力在2 s内的功不为零 |
| B．物体在2 s内的位移不为零 |
| C．物体在2 s末的速度为零 |
| D．以上说法都不正确 |
物体做匀加速直线运动，若第1秒内物体通过的位移是0.5m，则第2秒内的位移可能是（ ）
| A．0.6m | B．1.0m | C．1.4m | D．1.8m |
如图所示，小车向右做匀加速直线运动的加速度大小为a，bc是固定在小车上的水平横杆，物块M穿在杆上，M通过细线悬吊着小铁球m，M、m均相对小车静止，细线与竖直方向的夹角为θ。若小车的加速度逐渐增大到3a时，M、m仍与小车保持相对静止，则
| A．细线与竖直方向的夹角增加到原来的3倍 |
| B．细线与竖直方向夹角的正弦值增加到原来的3倍 |
| C．细线的拉力增加到原来的3倍 |
| D．M受到的摩擦力增加到原来的3倍 |
甲、乙两车某时刻由同一地点沿同一方向开始做直线运动，若以该时刻作为计时起点得到两车的位移一时间图象如图所示，则下列说法正确的是（ ）
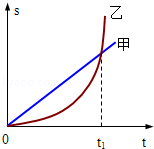
| A．t1时刻甲车从后面追上乙车 |
| B．t1时刻两车相距最远 |
| C．t1时刻两车的速度刚好相等 |
| D．0到t1时间内，两车的平均速度相等 |
某一时刻a、b两物体以不同的速度经过某一点，并沿同一方向做匀加速直线运动，已知两物体的加速度相同，则在运动过程中（ ）
| A．a、b两物体速度之差保持不变 |
| B．a、b两物体速度之差与时间成正比 |
| C．a、b两物体位移之差与时间成正比 |
| D．a、b两物体位移之差与时间平方成正比 |
一辆巡逻车最快能在10s内由静止匀加速到最大速度vm=50m/s，并能保持这个速度匀速行驶，问该巡逻车在平直的高速公路上由静止追上前方2000m处正以v=35m/s的速度匀速行驶的汽车，至少需要的时间为（ ）
| A．100s | B．120s | C．140s | D．150s |
一个质点做直线运动，原来v＞0，a>0，x>0，从某时刻开始把加速度均匀减小至零，则
| A．速度一直增大，直至加速度为零为止 |
| B．速度逐渐减小，直至加速度为零为止 |
| C．位移一直增大，直至加速度为零为止 |
| D．位移逐渐减小，直至加速度为零为止 |
关于打点计时器的使用，下列说法中不正确的是（ ）
| A．打点计时器应用低压交流电源，交流电频率为50Hz |
| B．纸带必须穿过限位孔，并注意把纸带压在复写纸的上面 |
| C．要先通电，后释放纸带，纸带通过后立即切断电源 |
| D．为减小摩擦，每次测量应先将纸带理顺 |
质点做直线运动的位移x与时间t的关系为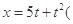
各物理量采用国际单位制单位）,则该质点（ ）
| A．第1 s内的位移是6 m |
| B．前2 s内的平均速度是7 m/s |
| C．任意相邻1 s内的位移差都是1 m |
| D．任意1 s内的速度增量都是2 m/s |
如图所示，小车静止在光滑水平地面上，小车的上表面由光滑的斜面AB和粗糙的平面BC组成（它们在B处由极短的光滑圆弧平滑连接），小车右侧与竖直墙壁之间连接着一个力传感器，当传感器受压力时，其示数为正值；当传感器受拉力时，其示数为负值。一个小滑块（可视为质点）从A点由静止开始下滑，经B至C点的过程中，传感器记录到的力F随时间t变化的关系如下面四图表示，其中可能正确的是（ ）
粤公网安备 44130202000953号