如图所示是一种研究劈的作用的装置,托盘A固定在细杆上,细杆放在固定的圆孔中,下端有滚轮,细杆只能在竖直方向上移动,在与托盘连接的滚轮正下面的底座上也固定一个滚轮,轻质劈放在两滚轮之间,劈背的宽度为a,侧面的长度为l,劈尖上固定的细线通过滑轮悬挂总质量为m的钩码,调整托盘上所放砝码的质量M,可以使劈在任何位置时都不发生移动.忽略一切摩擦和劈、托盘、细杆与滚轮的重力,若a= l,试求M是m的多少倍?
l,试求M是m的多少倍?
(22分)如图(a),小球甲固定于水平气垫导轨的左端,质量m=0.4kg的小球乙可在导轨上无摩擦地滑动,甲、乙两球之间因受到相互作用而具有一定的势能,相互作用力沿二者连线且随间距的变化而变化。现已测出势能随位置x的变化规律如图(b)中的实线所示。已知曲线最低点的横坐标x0=20cm,虚线①为势能变化曲线的渐近线,虚线②为经过曲线上某点的切线。

(1)将小球乙从x1=8cm处由静止释放,小球乙所能达到的最大速度为多大?
(2)假定导轨右侧足够长,将小球乙在导轨上从何处由静止释放,小球乙不可能第二次经过x0=20cm的位置?并写出必要的推断说明;
(3)若将导轨右端抬高,使其与水平面的夹角α=30°,如图(c)所示。将球乙从x2=6cm处由静止释放,小球乙运动到何处时速度最大?并求其最大速度;
(4)在图(b)上画出第(3)问中小球乙的动能Ek与位置x的关系图线。
(14分) 中国首艘航母“瓦良格”号即将投入使用,航母服役将成为“中国军队全面推进军事现代化进程的重大转折点”。为了减少战斗机起飞时在甲板上加速的时间和距离,现代航母大多采用了蒸汽弹射技术.一架总质量M=5.0x103kg的战机如果采用滑行加速(只依靠自身动力系统加速),要达到vo=60m/s的起飞速度,甲板水平跑道的长度至少为120m。采用蒸汽弹射技术,战机在自身动力和持续的蒸汽动力共同作用下只要水平加速60m就能达到起飞速度。假设战机起飞过程是匀加速直线运动,航母保持静止,空气阻力大小不变,取g=l0m/s2。
(1)采用蒸汽弹射技术,求战机加速过程中加速度大小以及质量m=60kg的飞行员受到座椅作用力的大小。
(2)采用蒸汽弹射技术,弹射系统的弹力为多大?弹力在加速60m的过程中对战机做的功是多少?
用弹簧秤称一物体的重力时,读数为7.5 N.把这个物体放在倾角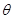 =37°的斜面上,用同样的弹簧秤平行于斜面拉着该物体向上做匀速运动时,弹簧秤的读数为6 N,求:
=37°的斜面上,用同样的弹簧秤平行于斜面拉着该物体向上做匀速运动时,弹簧秤的读数为6 N,求:
(1)斜面对物体的支持力大小.
(2)物体与斜面之间的动摩擦因数.
杂技中的“顶竿”由两个演员共同表演,站在地面上的演员肩部顶住一根长竹竿,另一演员爬至竹竿顶端完成各种动作后下滑.若竹竿上演员自竿顶由静止开始下滑,滑到竹竿底部时速度正好为零.已知竹竿底部与下面顶竿人肩部之间有一传感器,传感器显示竿上演员自竿顶滑下过程中顶竿人肩部的受力情况如图所示.竹竿上演员质量为m1="40" kg,竹竿质量m2="10" kg,取g="10" m/s2.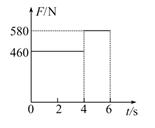
(1)求竹竿上的人下滑过程中的最大速度v1;
(2)请估测竹竿的长度h.
如图(a)所示,木板OA可绕轴O在竖直平面内转动,某研究小组利用此装置探索物块在方向始终平行于斜面、大小为F=8N的力作用下加速度与斜面倾角的关系。已知物块的质量m=1kg,通过DIS实验,得到如图(b)所示的加速度与斜面倾角的关系图线。若物块与木板间的动摩擦因数为0.2,假定物块与木板间的最大静摩擦力始终等于滑动摩擦力,g取10m/s2。试问:
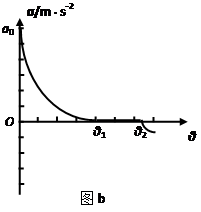
(1)图(b)中图线与纵坐标交点ao多大?
(2)图(b)中图线与θ轴交点坐标分别为θ1和θ2,木板处于该两个角度时的摩擦力指向何方?说明在斜面倾角处于θ1和θ2之间时物块的运动状态。
(3)θ1为多大?
(4)如果木板长L=2m,倾角为37°,物块在F的作用下由O点开始运动,为保证物块不冲出木板顶端,力F最多作用多长时间?(取sin37°=0.6,cos37°=0.8)
如图所示,拉B物的轻绳与竖直方向成60°角,O为一定滑轮,物体A与B间用跨过定滑轮的细绳相连且均保持静止,已知B的重力为100N,水平地面对B的支持力为80N,绳和滑轮质量及摩擦均不计,试求:
物体A的重力;
地面对物体B的摩擦力大小。
如图所示,质量为m的小球通过轻绳悬挂在一倾角为θ的光滑斜面上,轻绳与斜面平行,开始时系统处于静止状态。
(1)求系统静止时,绳对小球的拉力大小和斜面对小球的支持力大小。
(2)当系统以多大的加速度向左运动时,斜面对小球的支持力恰好为零?
如图所示,有两根轻杆OA、OB,A、B两端可绕竖直墙上的光滑转轴转动,O点悬挂100N的重物,OB杆水平且与OA杆成夹角30°,求OA杆、OB杆在O点受到的力的大小。
在水平地面上放一木板B,重力为G2=100N,再在木板上放一货箱A,重力为G1=500N,设货箱与木板、木板与地面的动摩擦因数μ均为0.5,先用绳子把货箱与墙拉紧,如下图所示,已知sinθ=0.6,cosθ=0.8,然后在木板B上施一水平力F,想把木板从货箱下抽出来,F至少应为多大?
在水平地面上放一木板B,重力为G2=100N,再在木板上放一货箱A,重力为G1=500N,设货箱与木板、木板与地面的动摩擦因数μ均为0.5,先用绳子把货箱与墙拉紧,如图所示,已知sinθ=3/5,cosθ=4/5,然后在木板B上施一水平力F,想把木板从货箱下抽出来,F至少应为多大?
当物体从高空下落时,空气阻力(不计空气的浮力)会随物体的速度增大而增大,因此经过一段距离后将匀速下落,这个速度称为此物体下落的终极速度.研究发现,在相同环境条件下,球形物体的终极速度仅与球的半径和质量有关.(g取10m/s2)下表是某次研究的实验数据:
| 小球编号 |
A |
B |
C |
| 小球的半径(×10-2m) |
0.5 |
0.5 |
1.5 |
| 小球的质量(×10-3kg) |
2 |
5 |
45 |
| 小球的终极速度(m/s) |
16 |
40 |
40 |
(1)根据表中的数据,求出B球与C球在达到终极速度时所受的空气阻力之比fB∶fC.
(2)根据表中的数据,归纳出球型物体所受的空气阻力f与球的终极速度v及球的半径r的关系,写出表达式并求出比例系数.

如图所示,图中弹簧Ⅰ和Ⅱ的劲度系数分别为 ,物体A和B的质量分别为
,物体A和B的质量分别为 .在弹性限度之内,悬挂平衡.现用一定的力沿竖直方向向上托起B,使两弹簧的长度之和恰等于两弹簧原自然长度之和.试求此时天花板对弹簧作用力F等于多大.
.在弹性限度之内,悬挂平衡.现用一定的力沿竖直方向向上托起B,使两弹簧的长度之和恰等于两弹簧原自然长度之和.试求此时天花板对弹簧作用力F等于多大.
如图所示,质量为m的正方体和质量为M的正方体放在两竖直墙和水平面间,处于静止状态。m与M相接触边与竖直方向的夹角为α,若不计一切摩擦,
求:(1)水平面对正方体M的弹力大小;
(2)墙面对正方体m的弹力大小.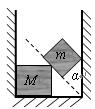
 已知T1时反应H2(g)+I2(g) 2HI(g) ; △H=-9.4 kJ/mol
已知T1时反应H2(g)+I2(g) 2HI(g) ; △H=-9.4 kJ/mol
(1)T1时,将2 mol HI(g)通入容积为2L的容器中发生上述反应,测得T1温度时各物质的物质的量随时间的变化关系如下表:
 物质 |
0 |
2 |
4 |
6 |
8 |
10 |
| H2 |
0 |
0.174 |
0.224 |
0.244 |
0.244 |
0.244 |
| I2[ |
0 |
0.174 |
0.224 |
0.244 |
0.244 |
0.244 |
| HI |
2 |
1.652 |
1.552 |
1.512 |
1.512 |
1.512 |
①前4 min,用HI(g)表示该反应的平均速率为 ; ②T1温度下,此反应H2(g)+I2(g) 2HI(g) 的平衡常数表达式为 ;
②T1温度下,此反应H2(g)+I2(g) 2HI(g) 的平衡常数表达式为 ;
③10分钟后,要使HI的转化率变为10%,可能的操作是 ;
A.扩大容积 B.同时减少三种物质各0.01 mol
C.加入HI(g) 1 mol D.降低温度 (2)如图,将2 mol HI(g)和2 molBr2(g)分别通入用光滑的滑动隔板隔离的同一容器的两边。加热容器升温至T2 ,反应足够长时间后,有关说法正确的是 。
(2)如图,将2 mol HI(g)和2 molBr2(g)分别通入用光滑的滑动隔板隔离的同一容器的两边。加热容器升温至T2 ,反应足够长时间后,有关说法正确的是 。
A.两边气体体积相同
B.两边气体颜色均比加热前变深
C.两边气体的平均相对分子质量均比加热前大
D.两边气体密度均比加热前减小