在水平地面上放一木板B,重力为G2=100N,再在木板上放一货箱A,重力为G1=500N,设货箱与木板、木板与地面的动摩擦因数μ均为0.5,先用绳子把货箱与墙拉紧,如图所示,已知sinθ=3/5,cosθ=4/5,然后在木板B上施一水平力F,想把木板从货箱下抽出来,F至少应为多大?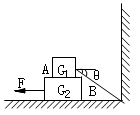
相关知识点
在水平地面上放一木板B,重力为G2=100N,再在木板上放一货箱A,重力为G1=500N,设货箱与木板、木板与地面的动摩擦因数μ均为0.5,先用绳子把货箱与墙拉紧,如图所示,已知sinθ=3/5,cosθ=4/5,然后在木板B上施一水平力F,想把木板从货箱下抽出来,F至少应为多大?